ЭЛЕКТРОННЫЙ ЛАБОРАТОРНЫЙ ПРАКТИКУМ
ПО УЧЕБНОМУ ПРЕДМЕТУ
"ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ"
№2. Решение задач линейного программирования с использованием графического метода
Цель: научить решать задачи линейного программирования графическим способом.
Оборудование: практикум, тетрадь для лабораторных и практических работ.
Литература:
- Колеснев В. И. Экономико-математические методы и модели в сфере АПК. Ч. 1. - Мн.: УМЦ, 2006. С. 40-43.
- Плотников А. Д. Математическое программирование: экспресс-курс. - Мн.: Новое знание, 2007. С. 33-44.
Время выполнения: 2 часа.
ВОПРОСЫ ВХОДНОГО КОНТРОЛЯ:
- Сформулируйте определение модели, математической модели.
- Приведите классификацию моделей.
- Приведите классификацию математических моделей.
- Приведите классификацию задач математического программирования.
- Приведите общий вид задачи линейного программирования.
- Назовите область, определяемую системой ограничений задачи линейного программирования
- Перечислите и опишите этапы составления математической модели.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:
Алгоритм графического решения задачи линейного программирования
1) построить область определения целевой функции;
2) построить направляющий вектор С = (с1, с2);
3) найти точку области допустимых решений, в которой целевая функция достигает экстремума;
4) найти экстремальное значение целевой функции.
Область определения целевой функции задается системой линейных равенств и неравенств. С графической точки зрения такая область представляет собой пересечение полуплоскостей (или прямых), которые определяются указанной системой. Во всех задачах линейного программирования область определения целевой функции всегда выпукла, т.е. вместе с любыми двумя точками этой же области принадлежат и точки отрезка, соединяющего эти две точки. В частном случае область определения может представлять собой неограниченную фигуру. В таком случае задача может не иметь решения ввиду неограниченности целевой функции.
Направляющий вектор С указывает направление возрастания целевой функции. Направляющий вектор имеет начало в начале координат, а конец — в точке (с1, с2), где с1 и с2 — значения коэффициентов при неизвестных х1 и х2 в целевой функции. Линия одного уровня (одного значения) целевой функции будет располагаться перпендикулярно направляющему вектору.
Оптимальное решение задачи находят, проведя линию одного уровня целевой функции перпендикулярно направляющему вектору и смещая ее в направлении, указанном вектором, при отыскании максимума и в обратном направлении при отыскании минимума функции. Смещают линию одного уровня в соответствующем направлении до тех пор, пока это возможно, т.е. когда при дальнейшем перемещении линии уровня она уже не будет иметь общих точек с областью допустимых решений.
Оптимальное решение задачи линейного программирования всегда будет находиться в угловой точке области. Если оптимум достигается в нескольких (двух — на плоскости) угловых точках, то имеет место альтернативный оптимум. Точные координаты соответствующей угловой точки можно найти, решив систему линейных уравнений, описывающих прямые, пересечение которых и образует данную угловую точку.
Экстремальное значение целевой функции вычисляют, подставив в ее аналитическое выражение найденное оптимальное решение (пару чисел х1 и х2).
МЕТОДИЧЕСКИЕ УКАЗАНИЯ:
Решить задачу линейного программирования графическим способом
F = x1 + x2 → min/max
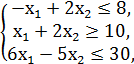
x1, x2 ≥ 0.
Решение. Введем на плоскости прямоугольную систему координат х1Ох2 и построим область определения целевой функции. Рассмотрим первое неравенство системы ограничений
-x1 + 2x2 ≤ 8.
Построим границу для полуплоскости, определяемой данным неравенством, для чего запишем уравнение
-x1 + 2x2 = 8.
Это уравнение прямой. Найдем координаты двух точек, лежащей на данной прямой
| х1 | х2 |
| 0 | 4 |
| -8 | 0 |
Следовательно прямая проходит через точки (0; 4) и (-8; 0). Построим ее на плоскости, обозначив римской цифрой I.
Определим теперь искомую полуплоскость. Для испытания возьмем точку (0; 0). Подставим координаты точки в уравнение прямой, получим
-0 + 2 ⋅ 0 ≤ 8,
т. е. данное неравенство выполняется. Следовательно искомая полуплоскость расположена по ту же сторону от прямой, что и начало координат. Отметим этот факт стрелкой на прямой I.
Рассмотрим второе неравенство системы ограничений
x1 + 2x2 ≥ 10.
Уравнение границы соответствующей полуплоскости
x1 + 2x2 = 10.
Найдем координаты двух точек, лежащей на данной прямой
| х1 | х2 |
| 0 | 5 |
| 10 | 0 |
Следовательно прямая проходит через точки (0; 5) и (10; 0). Построим ее на плоскости, обозначив римской цифрой II.
Для нахождения искомой полуплоскости испытаем начало координат (0; 0). Получим 0 + 2 ⋅ 0 ≥ 10, т. е. неравенство не выполняется, следовательно искомая полуплоскость расположена по другую сторону от прямой, чем начало координат. Отметим этот факт стрелкой на прямой II.
Рассмотрим третье неравенство системы ограничений
6x1 - 5x2 ≤ 30.
Уравнение границы соответствующей полуплоскости
6x1 - 5x2 = 30.
Найдем координаты двух точек, лежащей на данной прямой
| х1 | х2 |
| 0 | -6 |
| 5 | 0 |
Следовательно прямая проходит через точки (0; -6) и (5; 0). Построим ее на плоскости, обозначив римской цифрой III.
Для нахождения искомой полуплоскости испытаем начало координат (0; 0). Получим 6 ⋅ 0 - 5 ⋅ 0 ≤ 30, т. е. неравенство выполняется, следовательно искомая полуплоскость расположена по ту же сторону от прямой, что и начало координат. Отметим этот факт стрелкой на прямой III.
Дополнительно отметим стрелками тот факт, что область определения должна соответствовать условиям x1, x2 ≥ 0, т. е. она располагается в первом координатном угле.
Находим область определения целевой функции как пересечение найденных полуплоскостей. Этой областью будет являться заштрихованный треугольник.
Построим направляющий вектор С, начало которого находится в начале координат, конец - в точке (1; 1). Проведем линию одного уровня целевой функции перпендикулярно направляющему вектору С и будем смещать ее в направлении, противоположном направлению вектора (для поиска минимума целевой функции) или по направлению вектора (для поиска максимума целевой функции), до тех пор пока она имеет общие точки с областью определения целевой функции. Найденную точку, в которой достигается минимум целевой функции, обозначим min, точку, в которой достигается максимум - max.
Точка min образована пересечением граничных прямых I и II, для определения ее координат нужно решить систему линейных уравнений:
![]()
Отсюда находим х1 = 1, х2 = 4,5. Соответствующее значение целевой функции F(1; 4,5) = 1 + 4,5 = 5,5.
min: (1; 4,5) Fmin = 5,5.
Точка max образована пересечением граничных прямых I и III, для определения ее координат нужно решить систему линейных уравнений:
Отсюда находим х1 = 100/7, х2 = 78/7. Соответствующее значение целевой функции F(100/7; 78/7) =100/7 + 78/7 = 178/7.
max: (100/7; 78/7) Fmax = 178/7.
СОДЕРЖАНИЕ РАБОТЫ:
Вариант №1
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = x1 + 3x2 → min/max
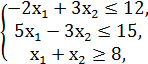
x1, x2 ≥ 0.
№2.
F = x1 + x2 → min/max
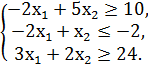
№3.
F = x1 + x2 → min/max
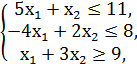
x1, x2 ≥ 0.
Вариант №2
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = 2x1 + x2 → min/max

x1, x2 ≥ 0.
№2.
F = 3x1 + 2x2 → min/max

№3.
F = x1 + x2 → min/max
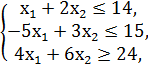
x1, x2 ≥ 0.
Вариант №3
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = x1 + x2 → min/max

x1, x2 ≥ 0.
№2.
F = x1 + 3x2 → min/max

№3.
F = 2x1 + x2 → min/max

x1, x2 ≥ 0.
Вариант №4
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = -x1 + x2 → min/max
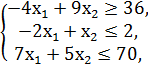
x1, x2 ≥ 0.
№2.
F = 3x1 + 2x2 → min/max
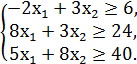
№3.
F = x1 + x2 → min/max
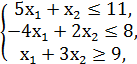
x1, x2 ≥ 0.
Вариант №5
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = x1 + x2 → min/max
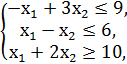
x1, x2 ≥ 0.
№2.
F = 4x1 + x2 → min/max
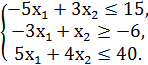
№3.
F = x1 + x2 → min/max
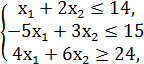
x1, x2 ≥ 0.
Вариант №6
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = x1 + x2 → min/max
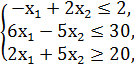
x1, x2 ≥ 0.
№2.
F = x1 + 3x2 → min/max
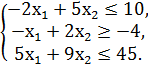
№3.
F = 2x1 + x2 → min/max
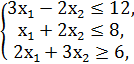
x1, x2 ≥ 0.
Вариант №7
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = x1 + x2 → min/max
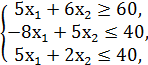
x1, x2 ≥ 0.
№2.
F = x1 + x2 → min/max

№3.
F = x1 + x2 → min/max
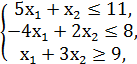
x1, x2 ≥ 0.
Вариант №8
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = x1 + 2x2 → min/max
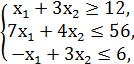
x1, x2 ≥ 0.
№2.
F = 3x1 + 2x2 → min/max
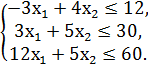
№3.
F = x1 + x2 → min/max
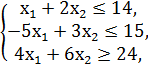
x1, x2 ≥ 0.
Вариант №9
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = -2x1 + x2 → min/max
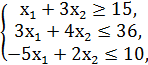
x1, x2 ≥ 0.
№2.
F = 4x1 + x2 → min/max
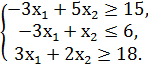
№3.
F = 2x1 + x2 → min/max
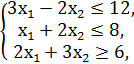
x1, x2 ≥ 0.
Вариант №10
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = x1 + x2 → min/max
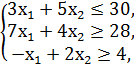
x1, x2 ≥ 0.
№2.
F = x1 + 3x2 → min/max
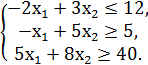
№3.
F = x1 + x2 → min/max
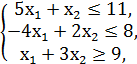
x1, x2 ≥ 0.
Вариант №11
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = x1 + 5x2 → min/max
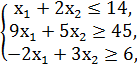
x1, x2 ≥ 0.
№2.
F = x1 + x2 → min/max
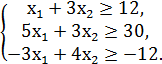
№3.
F = x1 + x2 → min/max
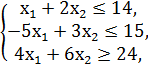
x1, x2 ≥ 0.
Вариант №12
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = x1 + x2 → min/max
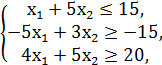
x1, x2 ≥ 0.
№2.
F = 5x1 + x2 → min/max
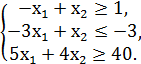
№3.
F = 2x1 + x2 → min/max

x1, x2 ≥ 0.
Вариант №13
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = x1 + x2 → min/max

x1, x2 ≥ 0.
№2.
F = x1 + 3x2 → min/max
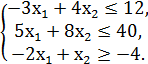
№3.
F = x1 + x2 → min/max

x1, x2 ≥ 0.
Вариант №14
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = x1 + 5x2 → min/max

x1, x2 ≥ 0.
№2.
F = 3x1 + 2x2 → min/max
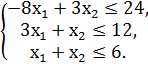
№3.
F = x1 + x2 → min/max
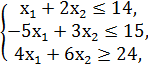
x1, x2 ≥ 0.
Вариант №15
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = 5x1 + x2 → min/max

x1, x2 ≥ 0.
№2.
F = x1 + 4x2 → min/max
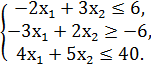
№3.
F = 2x1 + x2 → min/max
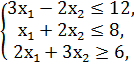
x1, x2 ≥ 0.
Вариант №16
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = x1 + x2 → min/max
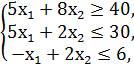
x1, x2 ≥ 0.
№2.
F = 4x1 + x2 → min/max
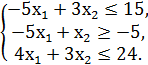
№3.
F = x1 + x2 → min/max
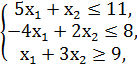
x1, x2 ≥ 0.
Вариант №17
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = -x1 + 2x2 → min/max
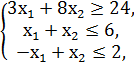
x1, x2 ≥ 0.
№2.
F = x1 + 3x2 → min/max
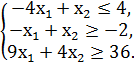
№3.
F = x1 + x2 → min/max
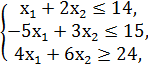
x1, x2 ≥ 0.
Вариант №18
Построить область определения целевой функции и графическим методом найти наибольшее и наименьшее значения функции в этой области.
№1.
F = x1 + x2 → min/max
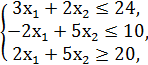
x1, x2 ≥ 0.
№2.
F = x1 + x2 → min/max
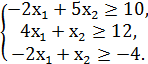
№3.
F = 2x1 + x2 → min/max

x1, x2 ≥ 0.
ВОПРОСЫ ВЫХОДНОГО КОНТРОЛЯ:
- Перечислите этапы решения задачи линейного программирования графическим методом.
- Опишите порядок построения области определения целевой функции.
- Опишите порядок нахождения экстремального значения целевой функции при решении задачи линейного программирования графическим способом.
- Опишите особые случаи решения задачи линейного программирования графическим способом.
ДОМАШНЕЕ ЗАДАНИЕ:
Выучить алгоритм оптимизации целевой функции графическим способом; особые случаи решения задачи линейного программирования.