ЭЛЕКТРОННЫЙ ЛАБОРАТОРНЫЙ ПРАКТИКУМ
ПО УЧЕБНОМУ ПРЕДМЕТУ
"ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ"
№4. Решение задач линейного программирования с использованием симплекс-метода
Цель: сформировать умение составлять опорный план и решать задачу линейного программирования симплексным методом.
Оборудование: практикум, тетрадь для лабораторных и практических работ.
Литература:
- Колеснев В. И. Экономико-математические методы и модели в сфере АПК. Ч. 1. - Мн.: УМЦ, 2006. С. 43-52.
- Плотников А. Д. Математическое программирование: экспресс-курс. - Мн.: Новое знание, 2007. С. 68-78.
Время выполнения: 2 часа.
ВОПРОСЫ ВХОДНОГО КОНТРОЛЯ:
- Опишите суть симплекс-метода решения задачи линейного программирования.
- Опишите процесс приведения задачи линейного программирования к канонической форме записи.
- Дайте определение базисного решения системы линейных уравнений.
- Дайте определение опорного решения задачи линейного программирования.
- Опишите процесс проверки опорного плана решения задачи линейного программирования на оптимальность.
- Объясните правило прямоугольника, используемое при решении систем линейных уравнений методом Жордана-Гаусса.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:
Алгоритм решения задачи линейного программирования симплексным методом (поиск максимума)
1) представить задачу линейного программирования в канонической форме;
2) определить исходное опорное решение;
3) получить нулевое уравнение (выразить имеющиеся в целевой функции базисные переменные через свободные, затем перенести все переменные в левую часть выражения);
4) составить симплекс-таблицу;
5) рассмотреть оценки свободных переменных. Если все оценки неотрицательны, то имеющееся опорное решение является оптимальным, в противном случае перейти к новому опорному решению;
6) выбрать в качестве разрешающего столбец, которому соответствует отрицательная оценка;
7) найти соотношения ai0/aip для всех aip ≥ 0, i = 1, 2, ... , m. В качестве разрешающей выбрать строку, которой соответствует наименьшее из найденных соотношений;
8) выполнить одну итерацию метода Жордана-Гаусса. Перейти к шагу 5.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ:
Решить задачу линейного программирования симплексным методом
F = x1 + 3x2 → max
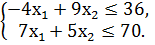
x1, x2 ≥ 0.
Решение. Представим задачу в канонической форме:
F = x1 + 3x2 → max

x1, x2, x3, x4 ≥ 0.
Исходное опорное решение Х = (0, 0, 36, 70).
Целевая функция не содержит базисных переменных. Получаем из нее нулевое уравнение
F - x1 - 3x2 = 0
Составляем симплекс-таблицу
СОДЕРЖАНИЕ РАБОТЫ:
Вариант №1
Решить задачи линейного программирования симплексным методом.
№1.
F = 2x1 + 4x2 → max,

x1, x2 ≥ 0.
№2.
F = 2x1 + 5x2 + x3 → max,
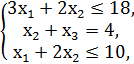
x1, x2, x3 ≥ 0.
Вариант №2
Решить задачи линейного программирования симплексным методом.
№1.
F = 4x1 + 10x2 → max,
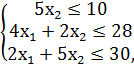
x1, x2 ≥ 0.
№2.
F = x1 + x2 + 5x3 → max,

x1, x2, x3 ≥ 0.
Вариант №3
Решить задачи линейного программирования симплексным методом.
№1.
F = 4x1 + 2x2 → max,
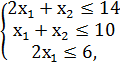
x1, x2 ≥ 0.
№2.
F = 3x1 + x2 + 2x3 → max,
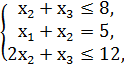
x1, x2, x3 ≥ 0.
Вариант №4
Решить задачи линейного программирования симплексным методом.
№1.
F = 6x1 + 3x2 → max,
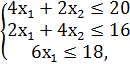
x1, x2 ≥ 0.
№2.
F = 4x1 + 4x2 + x3 → max,

x1, x2, x3 ≥ 0.
Вариант №5
Решить задачи линейного программирования симплексным методом.
№1.
F = 9x1 + 6x2 → max,
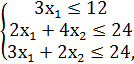
x1, x2 ≥ 0.
№2.
F = 4x1 + 5x2 + x3 → max,
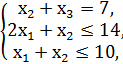
x1, x2, x3 ≥ 0.
Вариант №6
Решить задачи линейного программирования симплексным методом.
№1.
F = 6x1 + 8x2 → max,

x1, x2 ≥ 0.
№2.
F = 5x1 + 2x2 + x3 → max,
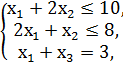
x1, x2, x3 ≥ 0.
Вариант №7
Решить задачи линейного программирования симплексным методом.
№1.
F = 2x1 + x2 → max,
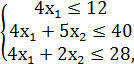
x1, x2 ≥ 0.
№2.
F = 5x1 + 5x2 + x3 → max,
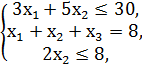
x1, x2, x3 ≥ 0.
Вариант №8
Решить задачи линейного программирования симплексным методом.
№1.
F = 6x1 + 4x2 → max,
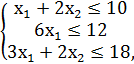
x1, x2 ≥ 0.
№2.
F = x1 + 5x2 + 2x3 → max,
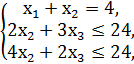
x1, x2, x3 ≥ 0.
Вариант №9
Решить задачи линейного программирования симплексным методом.
№1.
F = 10x1 + 4x2 → max,
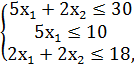
x1, x2 ≥ 0.
№2.
F = 7x1 + x2 + 4x3 → max,

x1, x2, x3 ≥ 0.
Вариант №10
Решить задачи линейного программирования симплексным методом.
№1.
F = 2x1 + 4x2 → max,
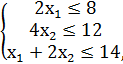
x1, x2 ≥ 0.
№2.
F = 5x1 + 5x2 + x3 → max,
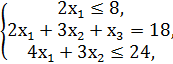
x1, x2, x3 ≥ 0.
Вариант №11
Решить задачи линейного программирования симплексным методом.
№1.
F = 4x1 + 6x2 → max,
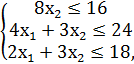
x1, x2 ≥ 0.
№2.
F = 3x1 + x2 + 6x3 → max,

x1, x2, x3 ≥ 0.
Вариант №12
Решить задачи линейного программирования симплексным методом.
№1.
F = 3x1 + 6x2 → max,
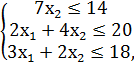
x1, x2 ≥ 0.
№2.
F = x1 + 3x2 + 2x3 → max,
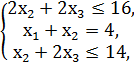
x1, x2, x3 ≥ 0.
Вариант №13
Решить задачи линейного программирования симплексным методом.
№1.
F = 8x1 + 4x2 → max,
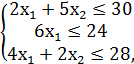
x1, x2 ≥ 0.
№2.
F = 4x1 + 3x2 + x3 → max,

x1, x2, x3 ≥ 0.
Вариант №14
Решить задачи линейного программирования симплексным методом.
№1.
F = 3x1 + 6x2 → max,
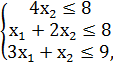
x1, x2 ≥ 0.
№2.
F = 2x1 + 6x2 + x3 → max,
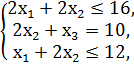
x1, x2, x3 ≥ 0.
Вариант №15
Решить задачи линейного программирования симплексным методом.
№1.
F = 4x1 + 2x2 → max,
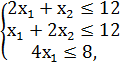
x1, x2 ≥ 0.
№2.
F = x1 + 2x2 + 2x3 → max,
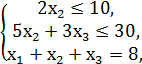
x1, x2, x3 ≥ 0.
Вариант №16
Решить задачи линейного программирования симплексным методом.
№1.
F = 2x1 + 4x2 → max,
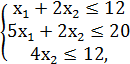
x1, x2 ≥ 0.
№2.
F = 5x1 + 5x2 + x3 → max,
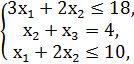
x1, x2, x3 ≥ 0.
Вариант №17
Решить задачи линейного программирования симплексным методом.
№1.
F = 4x1 + 10x2 → max,
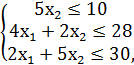
x1, x2 ≥ 0.
№2.
F = 5x1 + 3x2 + x3 → max,
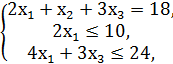
x1, x2, x3 ≥ 0.
Вариант №18
Решить задачи линейного программирования симплексным методом.
№1.
F = 4x1 + 2x2 → max,

x1, x2 ≥ 0.
№2.
F = x1 + 5x2 + 2x3 → max,

x1, x2, x3 ≥ 0.
ВОПРОСЫ ВЫХОДНОГО КОНТРОЛЯ:
- Опишите суть симплекс-метода решения задачи линейного программирования.
- Опишите процесс приведения задачи линейного программирования к канонической форме записи.
- Дайте определение базисного решения системы линейных уравнений.
- Дайте определение опорного решения задачи линейного программирования.
- Опишите процесс проверки опорного плана решения задачи линейного программирования на оптимальность.
- Расскажите о правилах выбора разрешающей строки и разрешающего столбца в симплекс-таблице.
ДОМАШНЕЕ ЗАДАНИЕ:
Выучить алгоритм решения задачи линейного программирования симплекс-методом.