ЭЛЕКТРОННЫЙ ЛАБОРАТОРНЫЙ ПРАКТИКУМ
ПО УЧЕБНОМУ ПРЕДМЕТУ
"ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ"
№6. Составление и решение двойственных задач
Цель: научить составлять и решать двойственные задачи.
Оборудование: практикум, тетрадь для лабораторных и практических работ.
Литература:
- Колеснев В. И. Экономико-математические методы и модели в сфере АПК. Ч. 1. - Мн.: УМЦ, 2006. С. 59-71.
- Плотников А. Д. Математическое программирование: экспресс-курс. - Мн.: Новое знание, 2007. С. 99-108.
Время выполнения: 2 часа.
ВОПРОСЫ ВХОДНОГО КОНТРОЛЯ:
- Опишите суть симплекс-метода решения задачи линейного программирования.
- Опишите процесс приведения задачи линейного программирования к канонической форме записи.
- Дайте определение базисного решения системы линейных уравнений.
- Дайте определение опорного решения задачи линейного программирования.
- Опишите процесс проверки опорного плана решения задачи линейного программирования на оптимальность.
- Объясните правило прямоугольника, используемое при решении систем линейных уравнений методом Жордана-Гаусса.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:
Правила составления двойственной задачи
1) число неизвестных прямой задачи равно числу ограничений двойственной;
2) матрицы коэффициентов систем ограничений получаются одна из другой транспонированием;
3) знаки неравенств противоположны, переменные в обеих задачах неотрицательны;
4) коэффициенты целевой функции прямой задачи являются свободными коэффициентами системы ограничений двойственной задачи и наоборот;
5) если в прямой задаче требуется найти максимум целевой функции, то в двойственной задаче - минимум и наоборот.
Основная теорема двойственности
Если одна из двух задач (прямая или двойственная) обладает оптимальным решением, то и другая задача также имеет решение, причем экстремальные значения целевой функции одной и другой задачи равны, например fmax = zmin. Если целевая функция одной из задач не ограничена, то другая задача также не имеет решения.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ:
Составить двойственную задачу к задаче линейного программирования
F = 3x1 - 5x2 - 3x3 - 5x4 + x5 → min
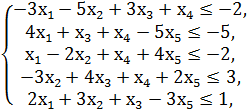
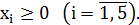
Решение. Обозначим неизвестные двойственной задачи у1, у2, у3, у4, у5 (число неизвестных двойственной задачи равно числу ограничений прямой). Составим целевую функцию, коэффициенты которой являются свободными коэффициентами системы ограничений прямой задачи, и заменим знак экстремума на противоположный
Z = -2у1 - 5у2 - 2у3 + 3у4 + у5 → mах
Для получения системы ограничений двойственной задачи транспонируем матрицу коэффициентов системы ограничений прямой задачи, знаки неравенств заменяем на противоположные
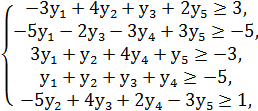
переменные двойственной задачи также неотрицательны
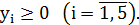
СОДЕРЖАНИЕ РАБОТЫ:
Вариант №1
1. Составить двойственную задачу к предложенной:
F = 30x1 - 28x2 - 4х3 → min
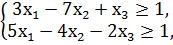
x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
Вариант №2
1. Составить двойственную задачу к предложенной:
F = -4x1 + 45x2 - 10х3 → min
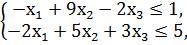
x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
Вариант №3
1. Составить двойственную задачу к предложенной:
F = 15x1 + 15x2 - 20х3 → min
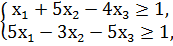
x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
Вариант №4
1. Составить двойственную задачу к предложенной:
F = 28x1 - 6x2 - 6х3 → min
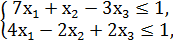
x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
Вариант №5
1. Составить двойственную задачу к предложенной:
F = -12x1 + 10x2 + 3х3 → min
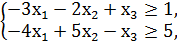
x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
Вариант №6
1. Составить двойственную задачу к предложенной:
F = -70x1 + 30x2 + 6х3 → min
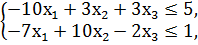
x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
Вариант №7
1. Составить двойственную задачу к предложенной:
F = -40x1 + 20x2 - 6х3 → min
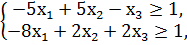
x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
Вариант №8
1. Составить двойственную задачу к предложенной:
F = 24x1 - 6x2 - 2х3 → min
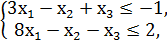
x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
Вариант №9
1. Составить двойственную задачу к предложенной:
F = 24x1 + 10x2 - 20х3 → min
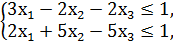
x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
Вариант №10
1. Составить двойственную задачу к предложенной:
F = -10x1 + 4x2 + 5х3 → min
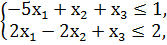
x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
Вариант №11
1. Составить двойственную задачу к предложенной:
F = 25x1 + 8x2 - 26х3 → min
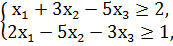
x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
Вариант №12
1. Составить двойственную задачу к предложенной:
F = -16x1 - 2x2 + 9х3 → min

x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
Вариант №13
1. Составить двойственную задачу к предложенной:
F = 40x1 + 6x2 + 8х3 → min
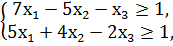
x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
Вариант №14
1. Составить двойственную задачу к предложенной:
F = -14x1 - 9x2 + 25х3 → min

x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
Вариант №15
1. Составить двойственную задачу к предложенной:
F = -12x1 + 10x2 + 6х3 → min
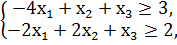
x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
Вариант №16
1. Составить двойственную задачу к предложенной:
F = 60x1 - 40x2 - 40х3 → min
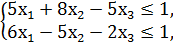
x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
Вариант №17
1. Составить двойственную задачу к предложенной:
F = -9x1 + 28x2 - 3х3 → min
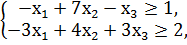
x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
Вариант №18
1. Составить двойственную задачу к предложенной:
F = 15x1 - 36x2 - 10х3 → min
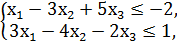
x1, x2, x3 ≥ 0.
2. Решить составленную задачу графическим методом.
3. Решить составленную задачу симплексным методом.
4. Сравнить полученные результаты.
ВОПРОСЫ ВЫХОДНОГО КОНТРОЛЯ:
- Какие задачи называются взаимно двойственными?
- Перечислите правила составления двойственной задачи.
- Сформулируйте основную теорему двойственности.
- Интерпретируйте двойственную задачу с экономической точки зрения.
ДОМАШНЕЕ ЗАДАНИЕ:
Выучить правила составления двойственной задачи; основную теорему двойственности; экономический смысл двойственной задачи.