ЭЛЕКТРОННЫЙ ЛАБОРАТОРНЫЙ ПРАКТИКУМ
ПО УЧЕБНОМУ ПРЕДМЕТУ
"ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ"
№11. Решение задачи построения остовного дерева минимального веса с использованием алгоритмов Прима и Краскала
Цель: научить строить остовное дерево минимального веса.
Оборудование: практикум, тетрадь для лабораторных и практических работ.
Литература:
- Кристофидес Н. Теория графов. Алгоритмический подход. - М.: Мир, 1979. С. 11-28, 158-166.
- Новиков Ф. А. Дискретная математика для программистов. - СПб.: Питер, 2000. С. 189-209, 255-259.
- Таха, Хемди. Введение в исследование операций - М.: Издательский дом "Вильямс", 2005. С. 243-250.
Время выполнения: 2 часа.
ВОПРОСЫ ВХОДНОГО КОНТРОЛЯ:
- Дайте определение графа, приведите примеры.
- Дайте определение дерева, приведите примеры.
- Дайте определение остовного дерева графа, приведите примеры.
- Дайте определение минимального остовного дерева графа.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:
Граф называется деревом, если он является связным и не имеет циклов.
Остовом связного графа называется любой его подграф, содержащий все вершины графа и являющийся деревом.
Остовное дерево связного нагруженного графа с минимальной суммой длин содержащихся в нем ребер, называется минимальным остовным деревом графа.
Алгоритм Краскала
1) начать с несвязного графа Т, множество вершин которого идентично множеству вершин искомого графа G;
2) упорядочить ребра графа G в порядке неубывания их весов;
3) начав с первого ребра в списке, добавлять ребра в граф Т, причем добавление ребра не должно приводить к появлению циклов;
4) выполнять пункт 3 до тех пор пока в графе Т не останется изолированных вершин.
Полученный граф Т является минимальным остовным деревом графа G.
Алгоритм Прима
1) пусть минимальное остовное дерево Т состоит из одной произвольно выбранной вершины;
2) для каждой вершины уi, не принадлежащей остовному дереву, найти смежную с ней вершину хi, принадлежащую остовному дереву, вес ребра ri до которой минимален, и приписать вершине уiпометку (хi, ri). Если таких вершин хi нет, то приписать вершине уi пометку (0, ∞);
3) выбрать вершину уi* с минимальной пометкой ri, присоединить ее к минимальному остовному дереву через вершину хi. Если все вершины графа G занесены в минимальное остовное дерево Т, то остановиться, иначе перейти к следующему шагу алгоритма;
4) для всех вершин уi, смежных с вершиной уi*, обновить пометки, если текущая пометка ri больше расстояния сi от уi до уi*. Новая пометка будет иметь вид (уi*, сi). Перейти к шагу 3.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ:
1. Построить для заданного графа минимальное остовное дерево, используя алгоритм Краскала
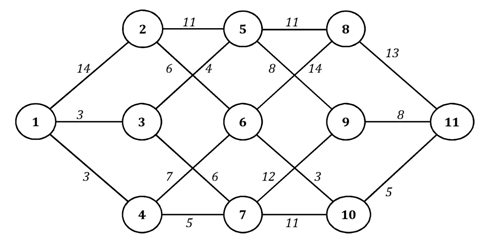
Решение.
2. Построить для заданного графа минимальное остовное дерево, используя алгоритм Прима

Решение.
СОДЕРЖАНИЕ РАБОТЫ:
Вариант №1
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.
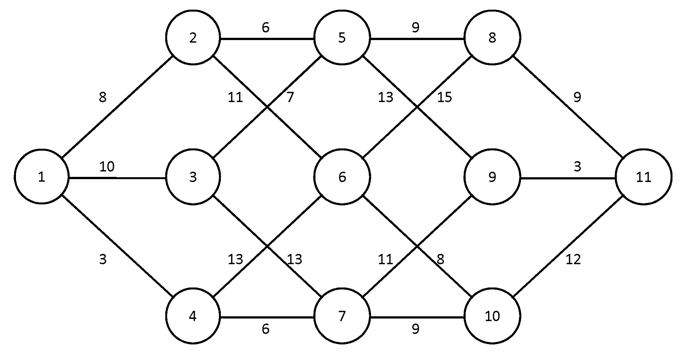
№2.
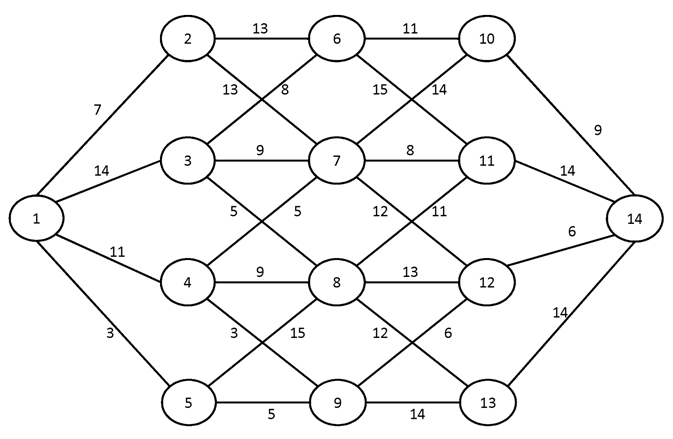
№3.
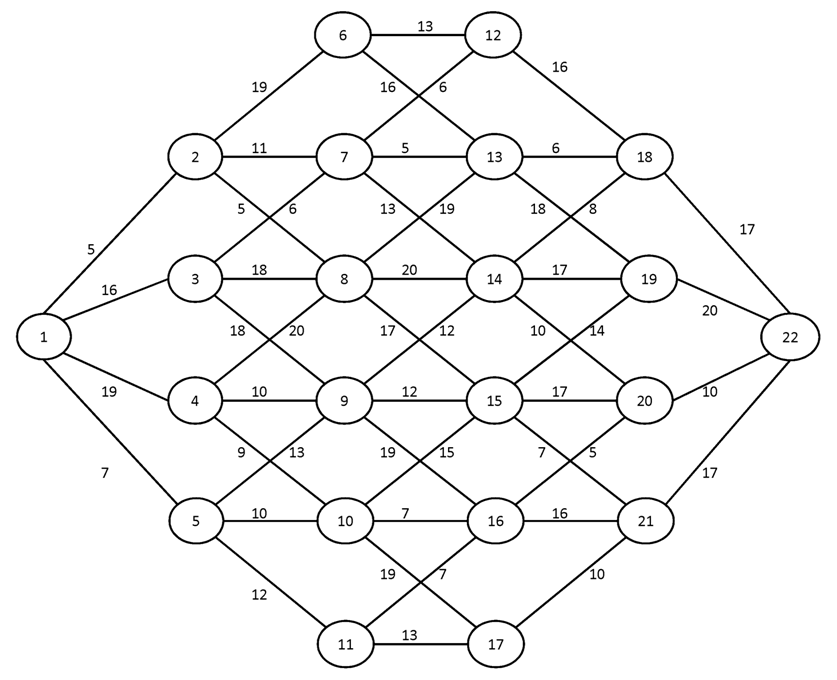
Вариант №2
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.
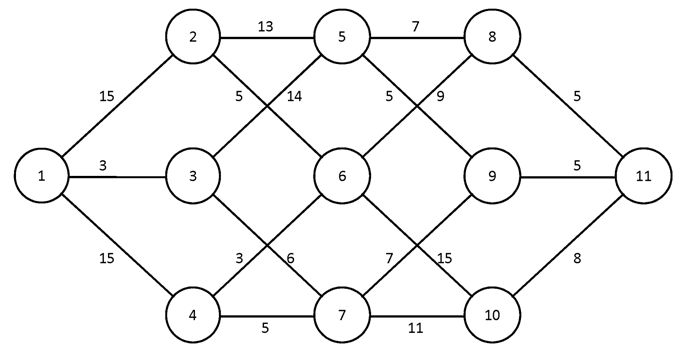
№2.
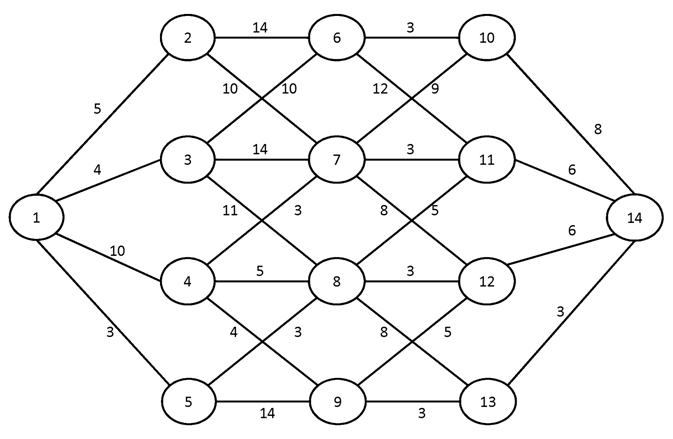
№3.
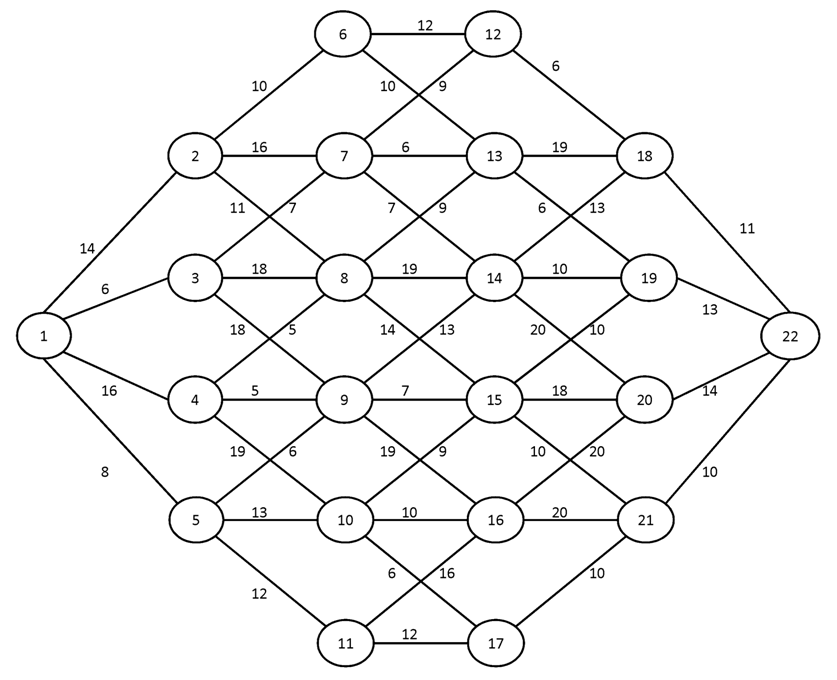
Вариант №3
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.
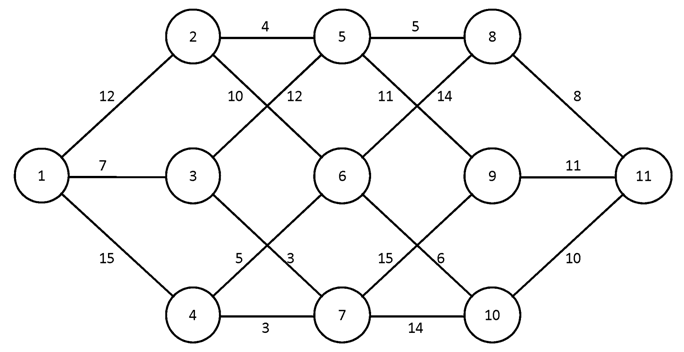
№2.
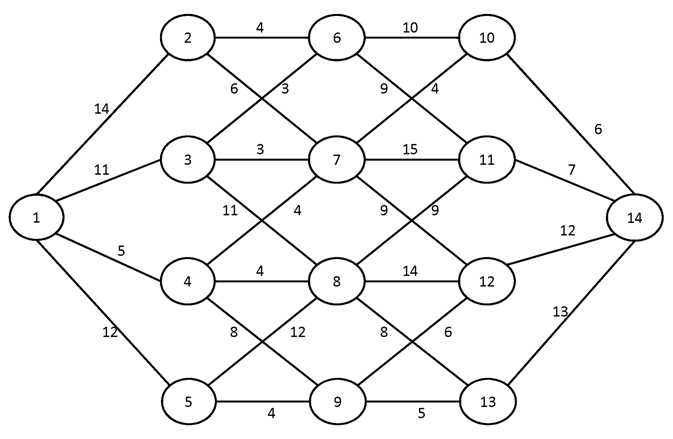
№3.
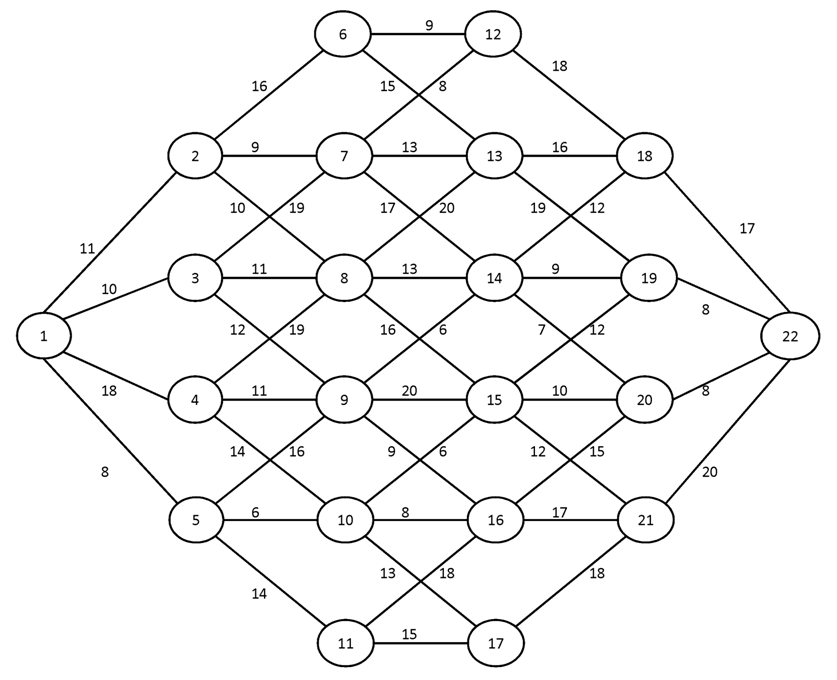
Вариант №4
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.
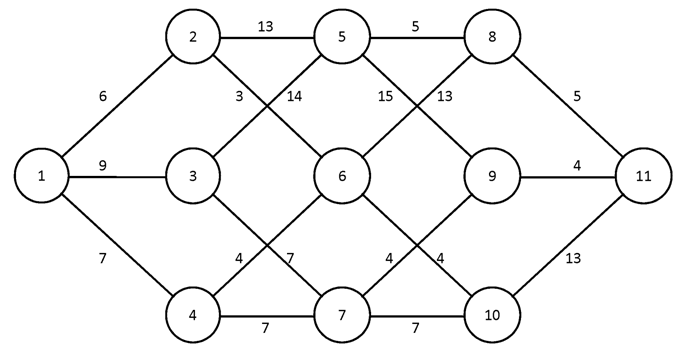
№2.
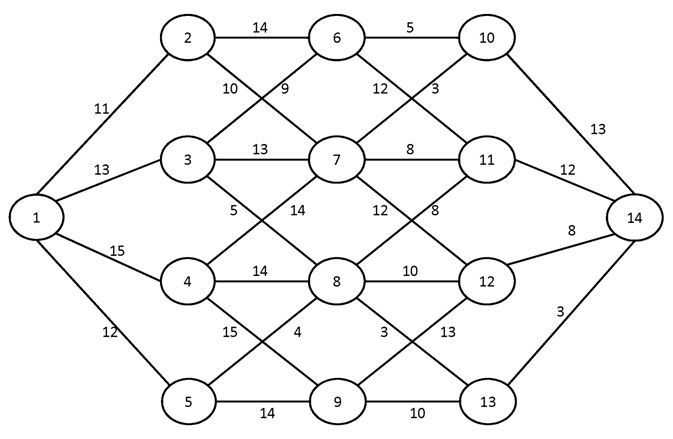
№3.
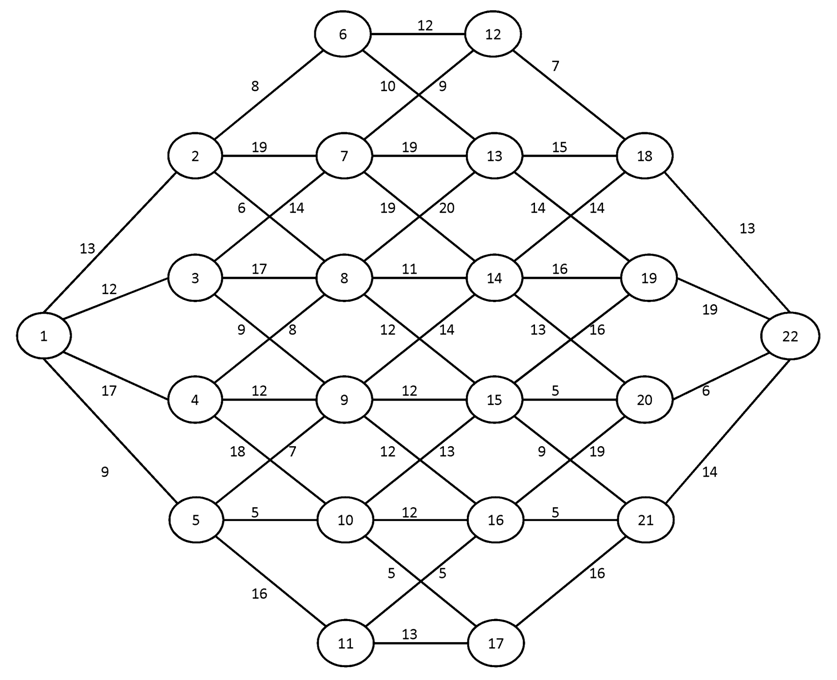
Вариант №5
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.
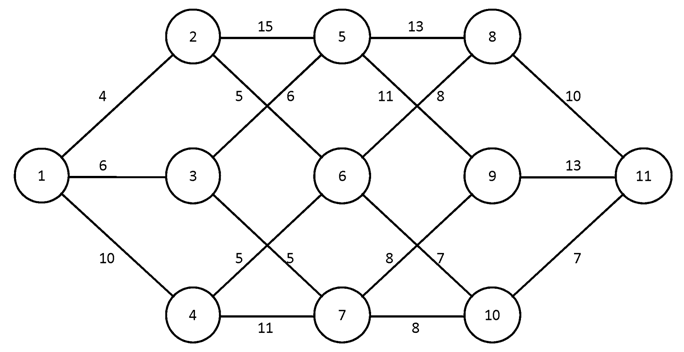
№2.
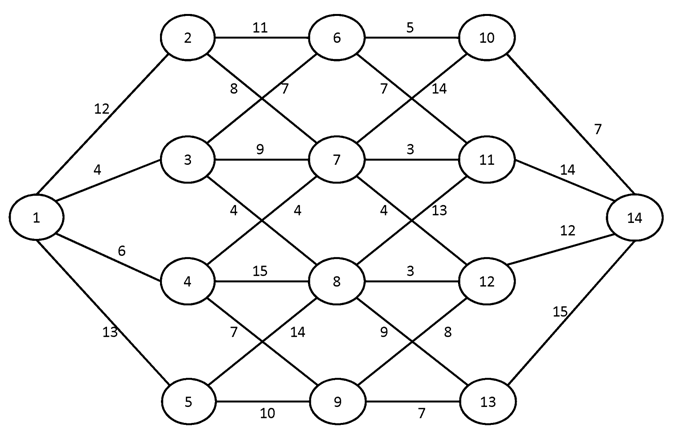
№3.
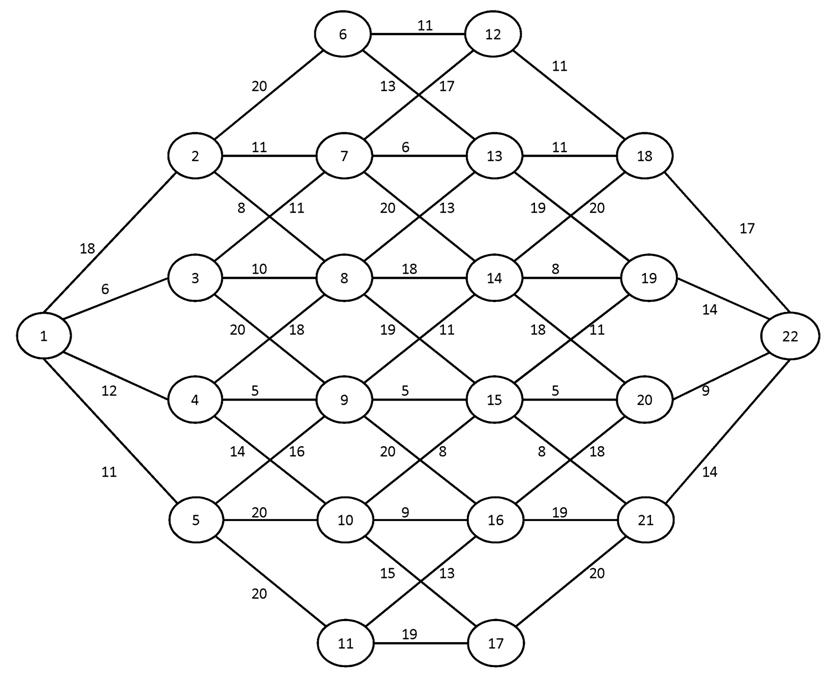
Вариант №6
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.
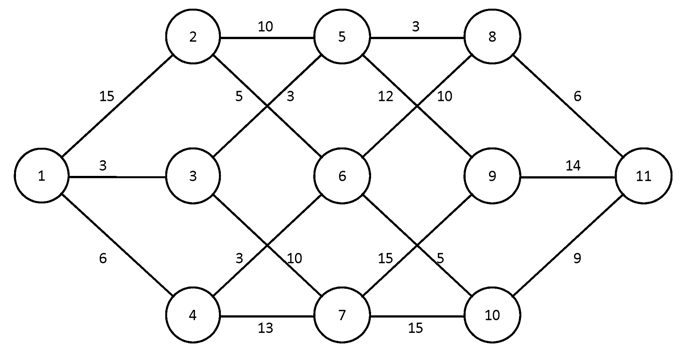
№2.
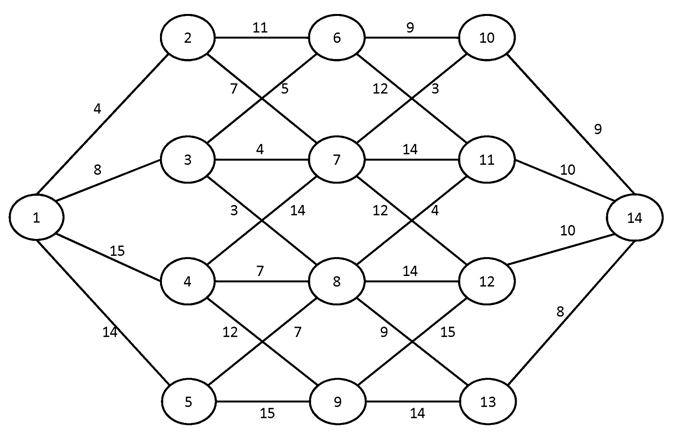
№3.

Вариант №7
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.

№2.
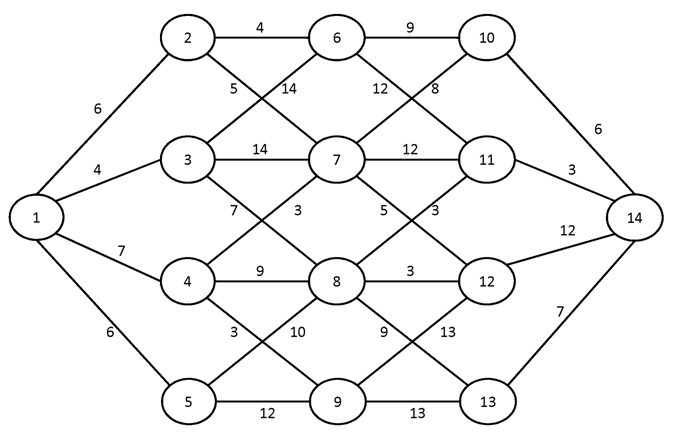
№3.
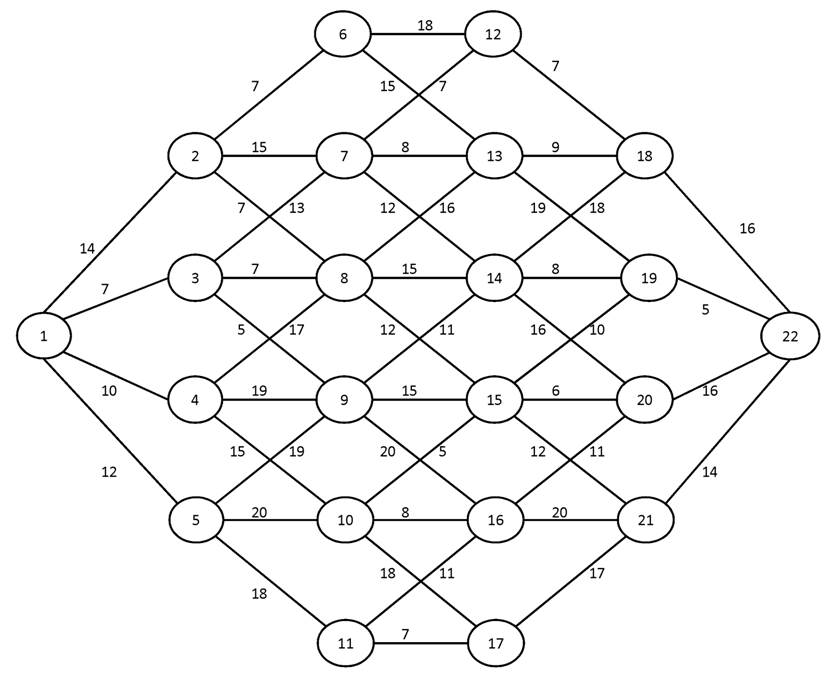
Вариант №8
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.
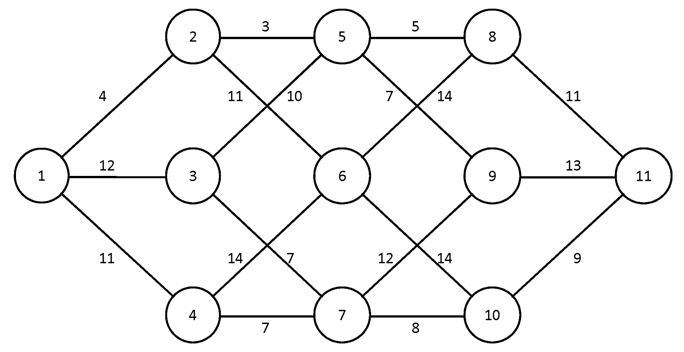
№2.
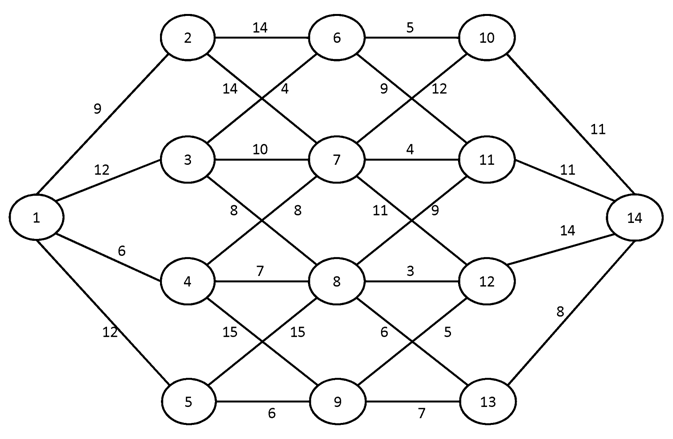
№3.
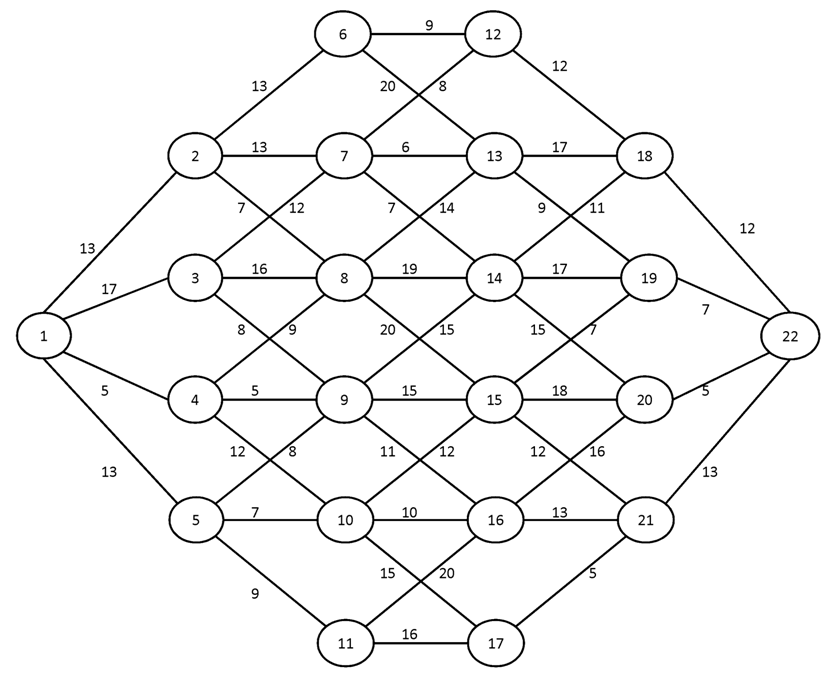
Вариант №9
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.
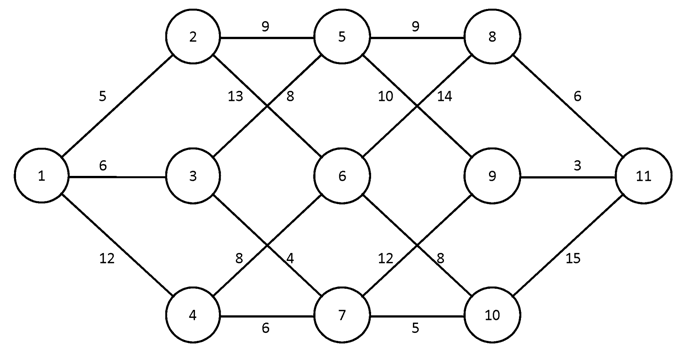
№2.
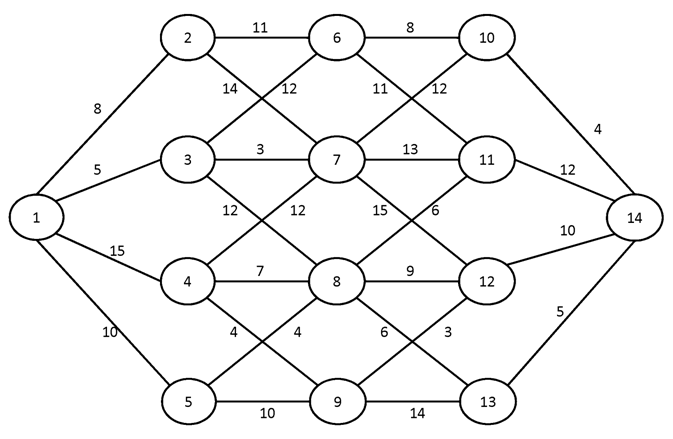
№3.
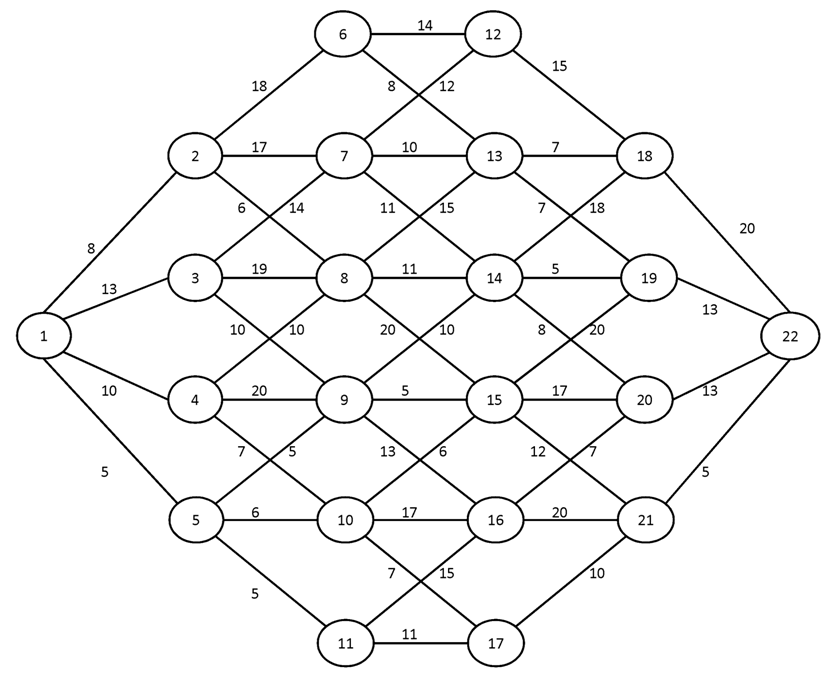
Вариант №10
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.
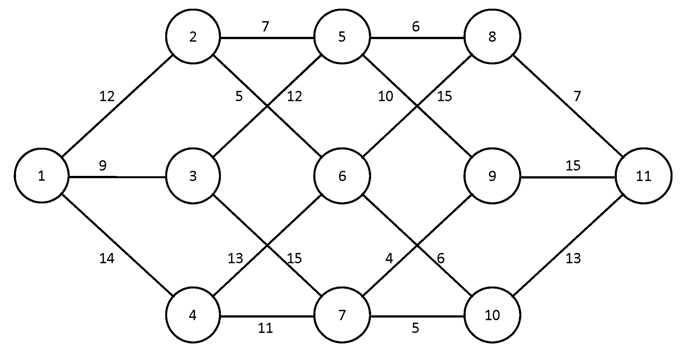
№2.

№3.
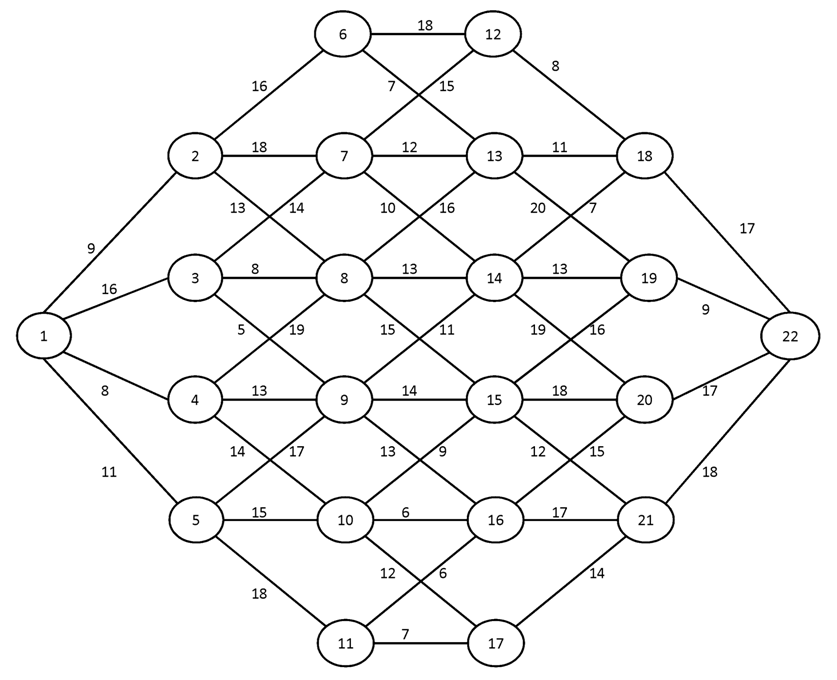
Вариант №11
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.
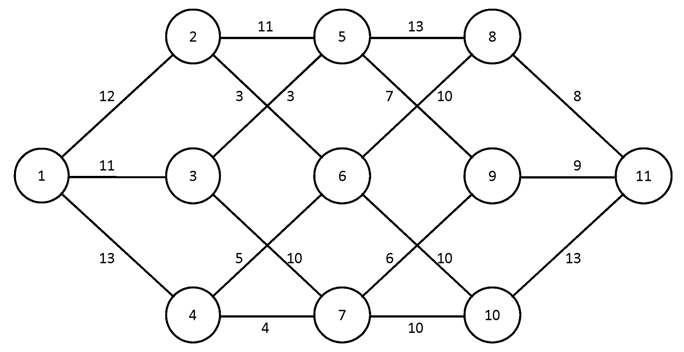
№2.
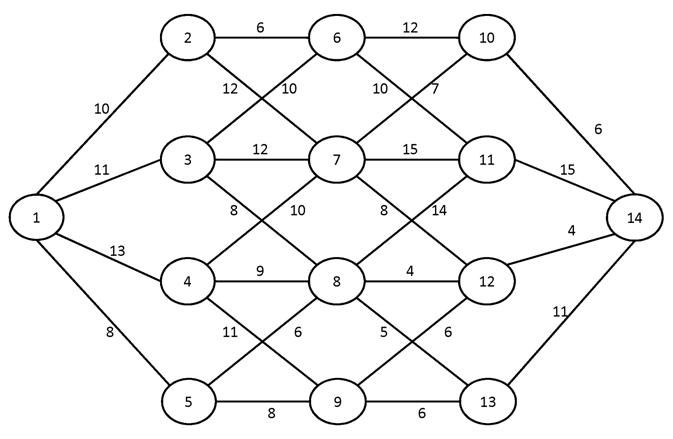
№3.
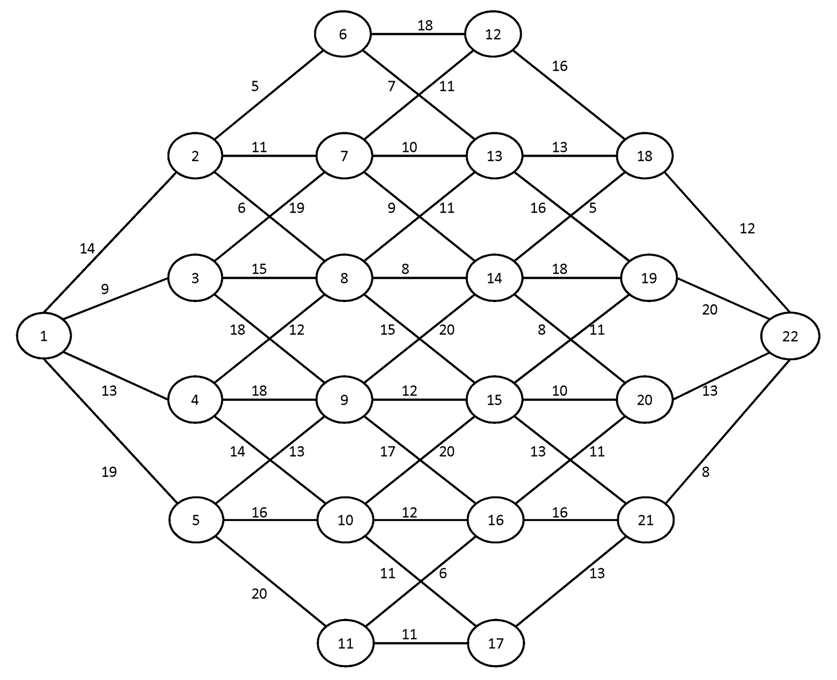
Вариант №12
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.
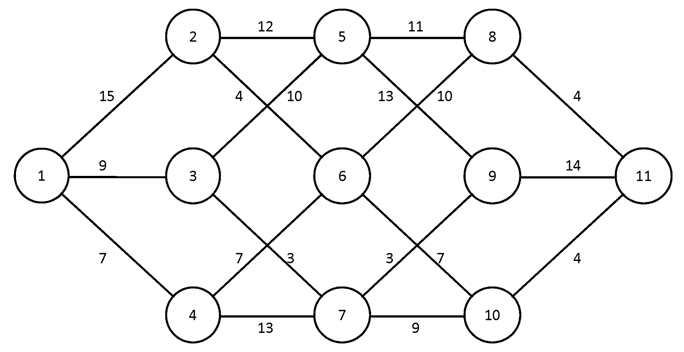
№2.

№3.
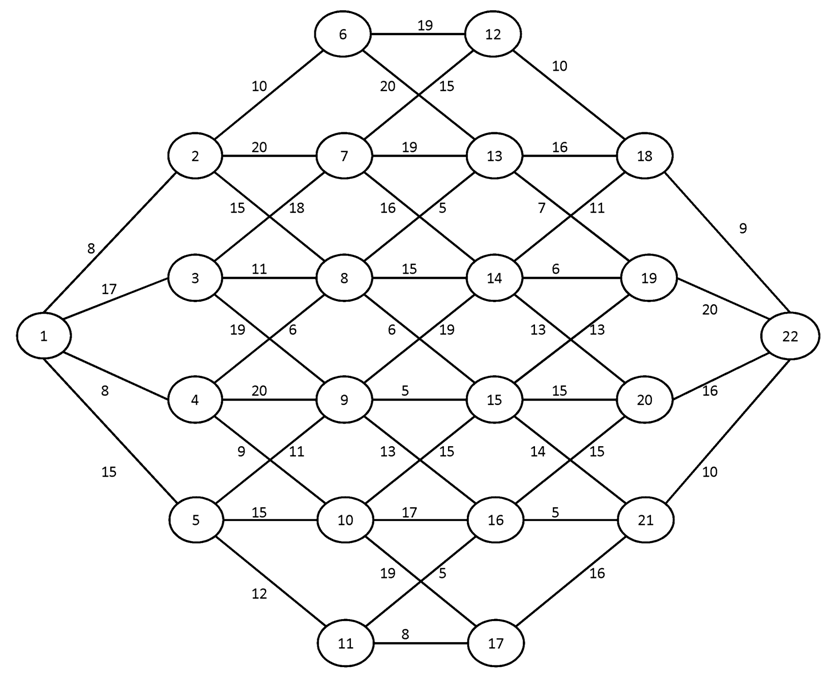
Вариант №13
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.
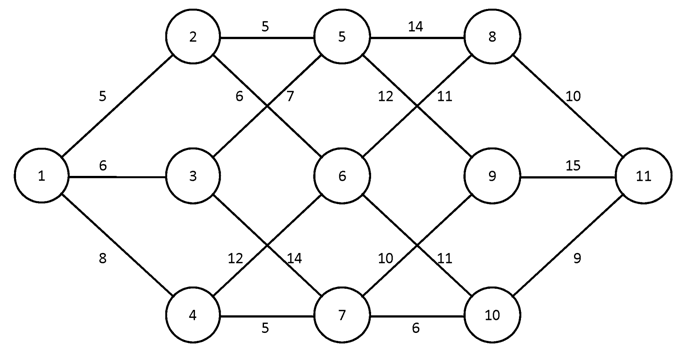
№2.
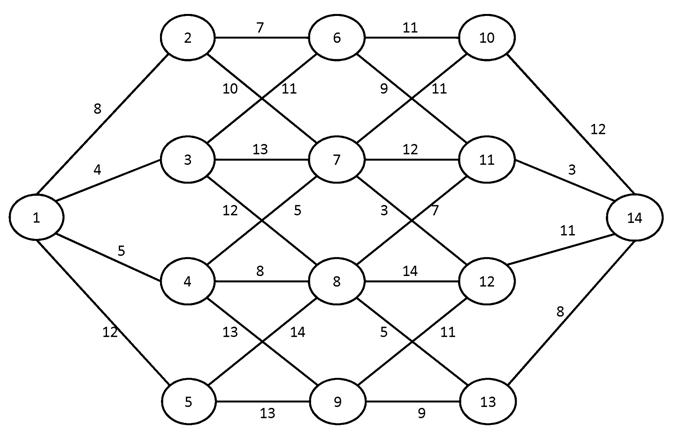
№3.
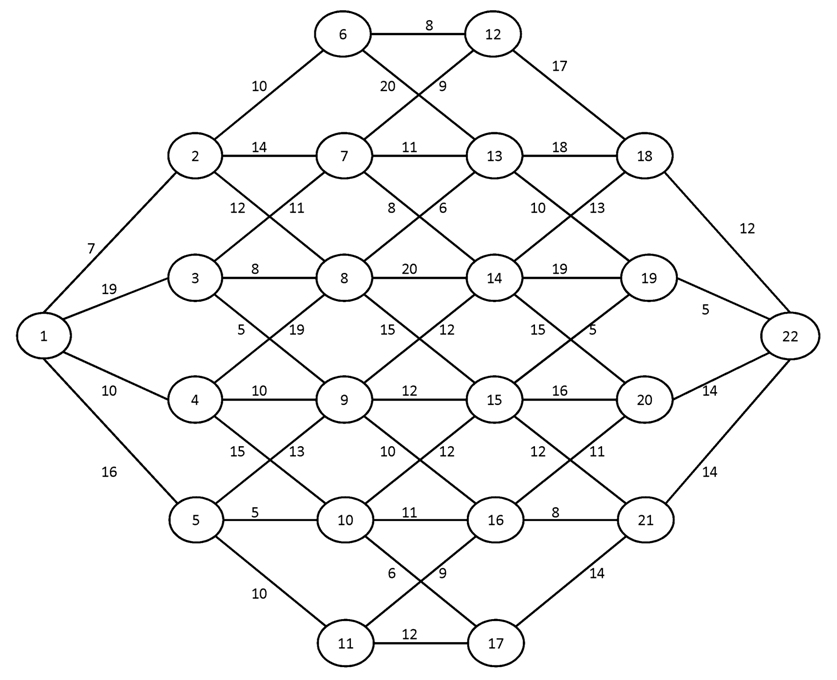
Вариант №14
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.
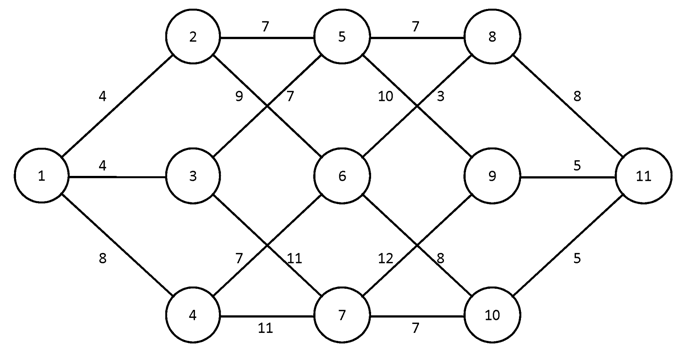
№2.
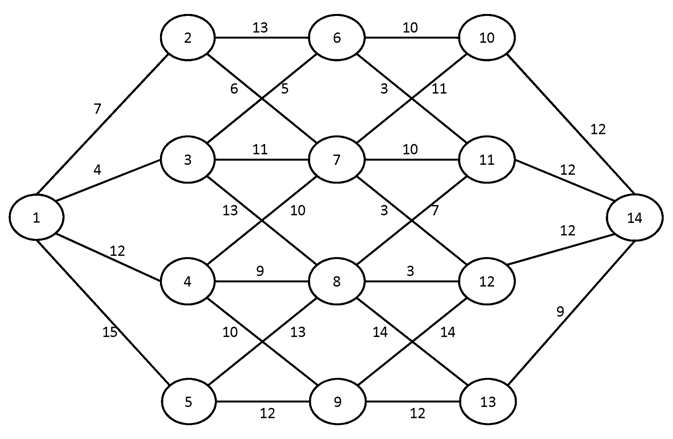
№3.
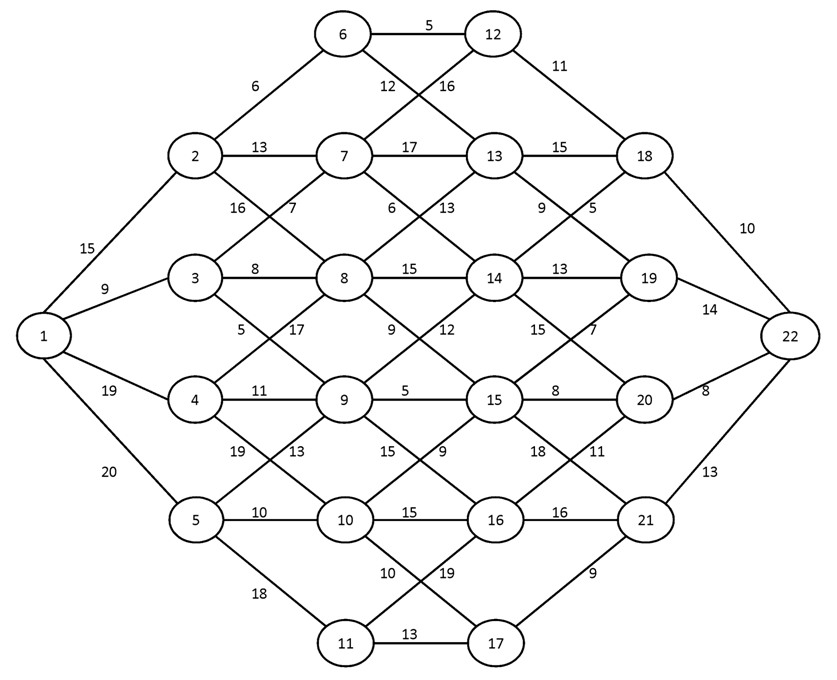
Вариант №15
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.
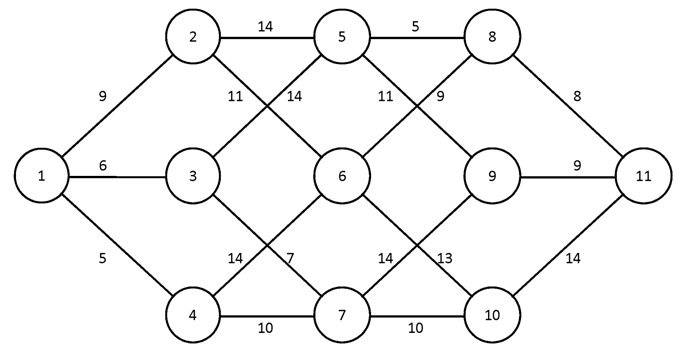
№2.
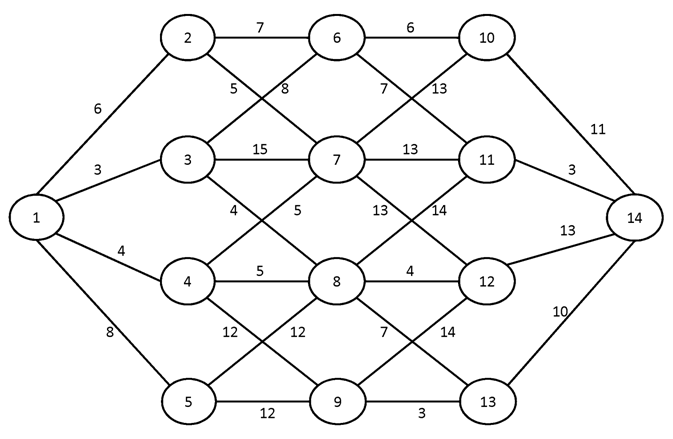
№3.
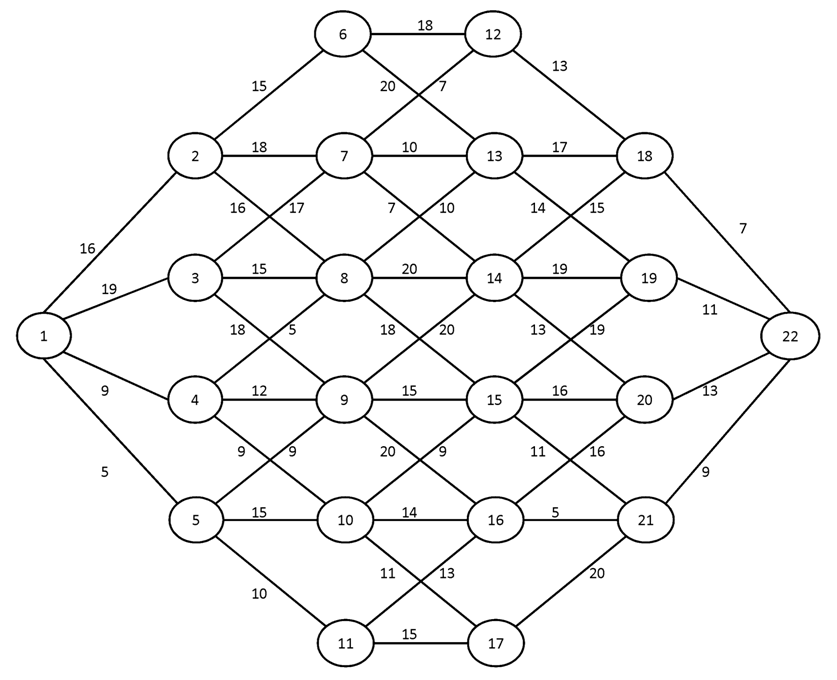
Вариант №16
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.
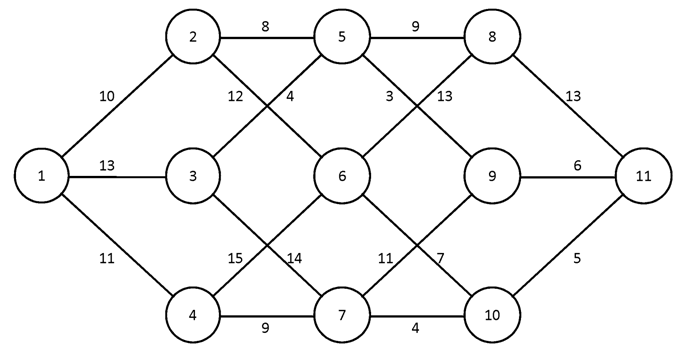
№2.

№3.
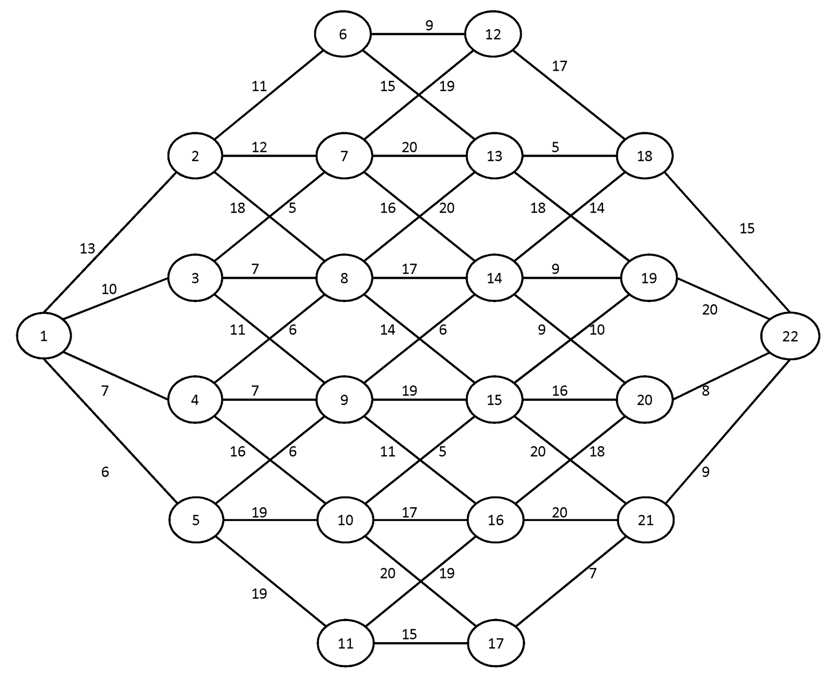
Вариант №17
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.
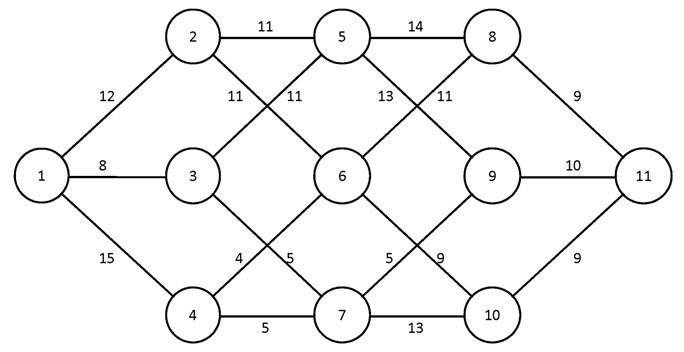
№2.
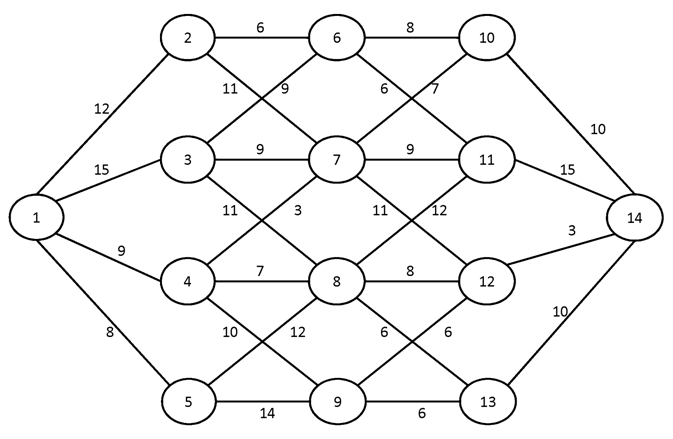
№3.
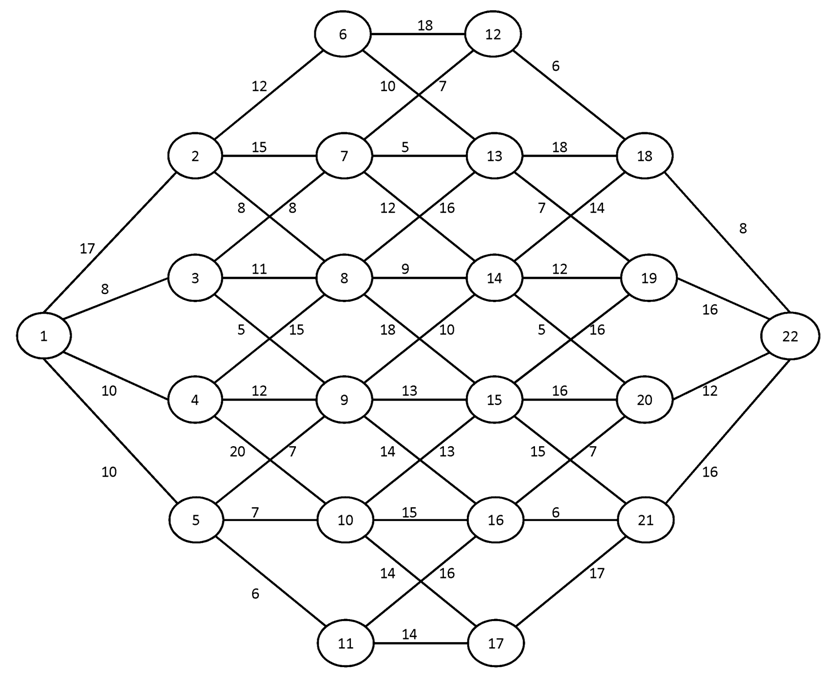
Вариант №18
Построить для заданного графа минимальные остовные деревья, используя алгоритмы Краскала и Прима. Сравните полученные результаты.
№1.
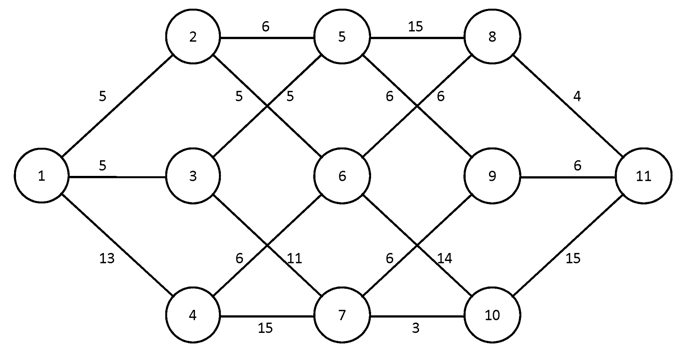
№2.
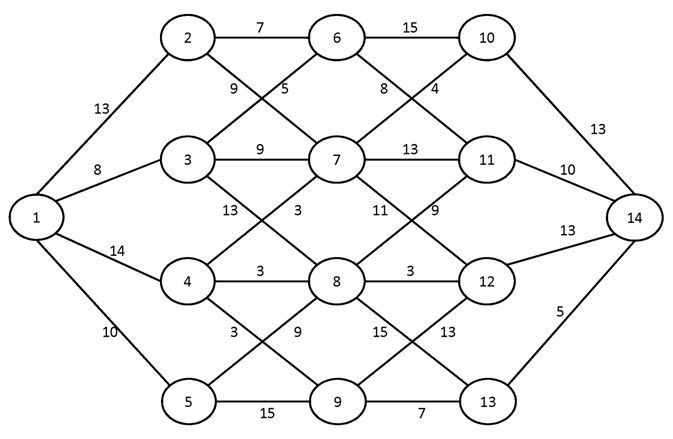
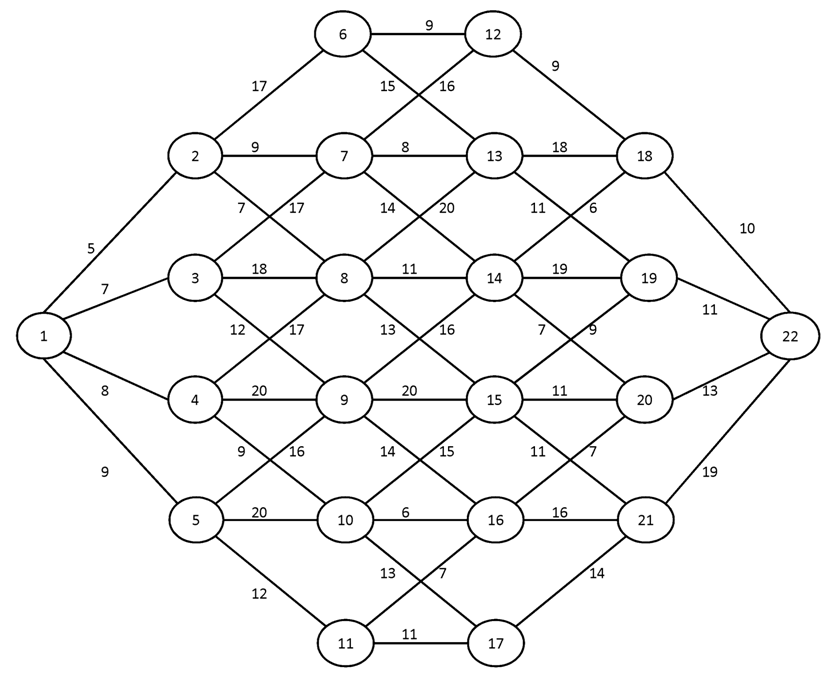
№3.
ВОПРОСЫ ВЫХОДНОГО КОНТРОЛЯ:
- Дайте определение графа, приведите примеры.
- Дайте определение дерева, приведите примеры.
- Дайте определение остовного дерева графа, приведите примеры.
- Дайте определение минимального остовного дерева графа.
- Опишите алгоритм Краскала.
- Опишите алгоритм Прима.
ДОМАШНЕЕ ЗАДАНИЕ:
Выучить алгоритм Краскала; алгоритм Прима.