ЭЛЕКТРОННЫЙ ЛАБОРАТОРНЫЙ ПРАКТИКУМ
ПО УЧЕБНОМУ ПРЕДМЕТУ
"ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ"
№12. Решение задачи нахождения кратчайшего пути в графе с использованием алгоритма Дейкстры
Цель: научить находить кратчайший путь в графе при помощи алгоритма Дейкстры.
Оборудование: практикум, тетрадь для лабораторных и практических работ.
Литература:
- Кристофидес Н. Теория графов. Алгоритмический подход. - М.: Мир, 1979. С. 175-189.
- Новиков Ф. А. Дискретная математика для программистов. - СПб.: Питер, 2000. С. 228-232.
- Таха, Хемди. Введение в исследование операций - М.: Издательский дом "Вильямс", 2005. С. 250-265.
Время выполнения: 2 часа.
ВОПРОСЫ ВХОДНОГО КОНТРОЛЯ:
- Дайте определение графа, приведите примеры.
- Сформулируйте определение пути (маршрута).
- Дайте понятие кратчайшего пути.
- Сформулируйте постановку задачи нахождения кратчайшего пути от заданного узла до всех остальных узлов в графе.
- Объясните суть алгоритма Дейкстры.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:
Алгоритм Дейкстры разработан для поиска кратчайшего пути между заданным исходным узлом и любым другим узлом сети. В процессе выполнения этого алгоритма при переходе от узла i к следующему узлу j используется специальная процедура пометки ребер. Обозначим через ui кратчайшее расстояние от исходного узла 1 до узла i, через dij — длину ребра (i, j). Тогда для узла j определим метку [uj, i] следующим образом.
[uj, i] = [ui + dij, i], dij > 0
Метки узлов в алгоритме Дейкстры могут быть двух типов: временные и постоянные. Временная метка впоследствии может быть заменена на другую временную, если будет найден более короткий путь к данному узлу. Когда же станет очевидным, что не существует более короткого пути от исходного узла к данному, статус временной метки изменяется на постоянный.
Алгоритм Дейкстры
1) Исходному узлу (узел 1) присваивается постоянная метка [0, —]. Полагаем i = 1;
2) Вычисляются временные метки [ui + dij, i] для всех узлов j, которые можно достичь непосредственно из узла i и которые не имеют постоянных меток. Если узел j уже имеет метку [uj, k], полученную от другого узла k, и, если ui + dij < uj, тогда метка [uj, k] заменяется на [ui + dij, i].
3) Если все узлы имеют постоянные метки, процесс вычислений заканчивается. В противном случае выбирается метка [ur, s] с наименьшим значением расстояния ur среди всех временных меток (если таких меток несколько, то выбор произволен). Полагаем i = r и повторяем этап 2.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ:
- Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
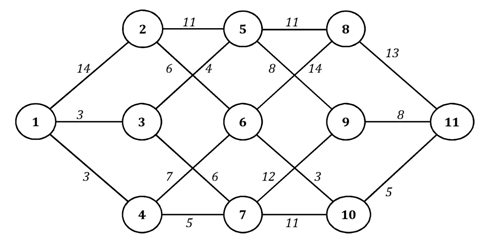
Решение.
СОДЕРЖАНИЕ РАБОТЫ:
Вариант №1
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.
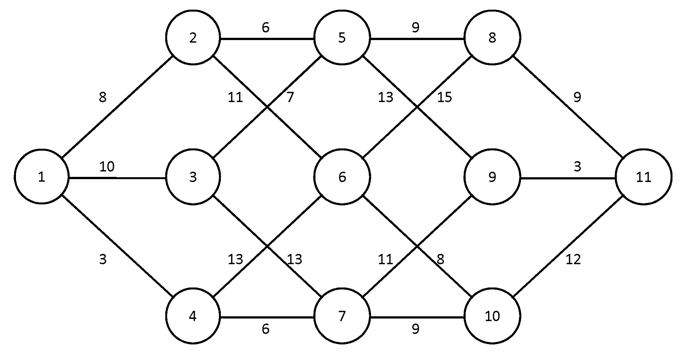
№2.
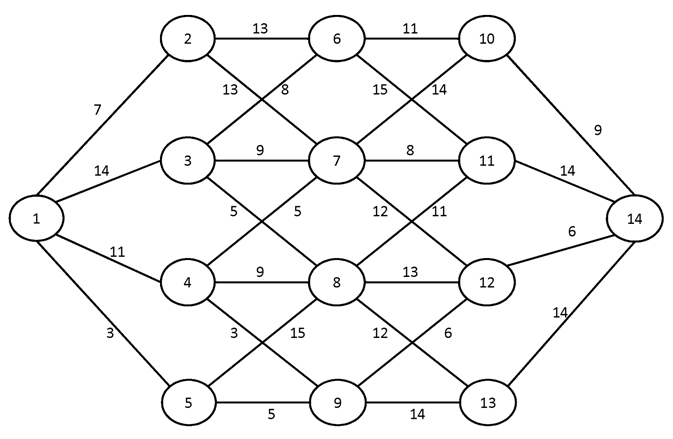
№3.
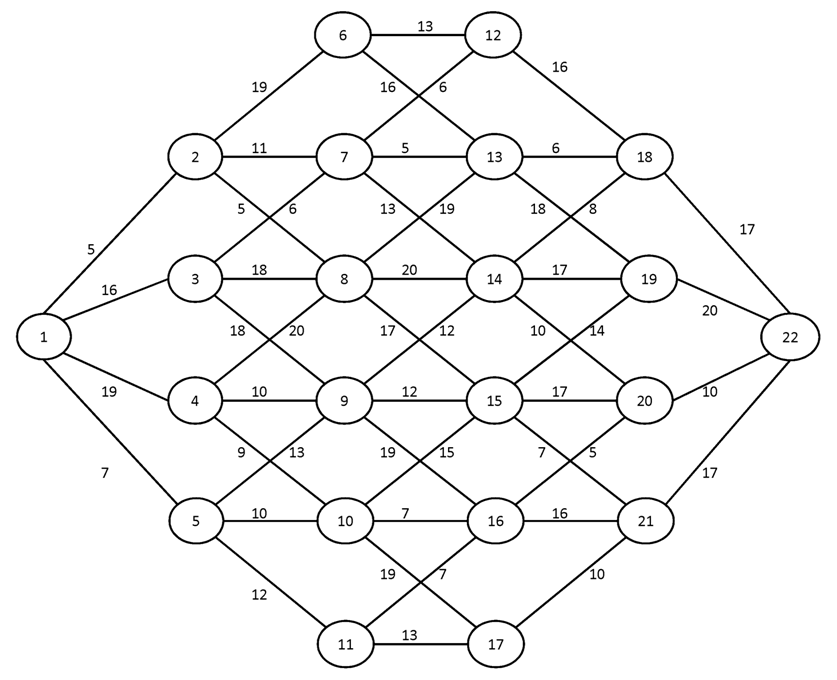
Вариант №2
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.
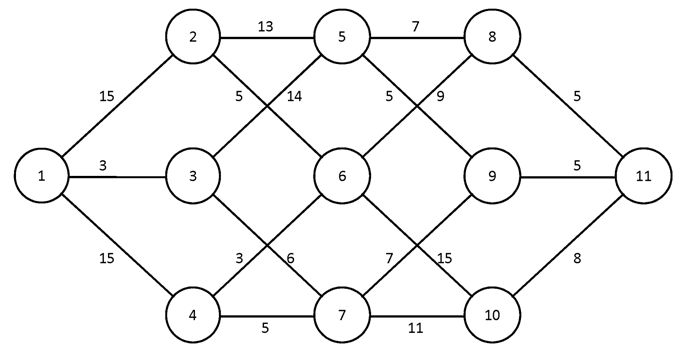
№2.
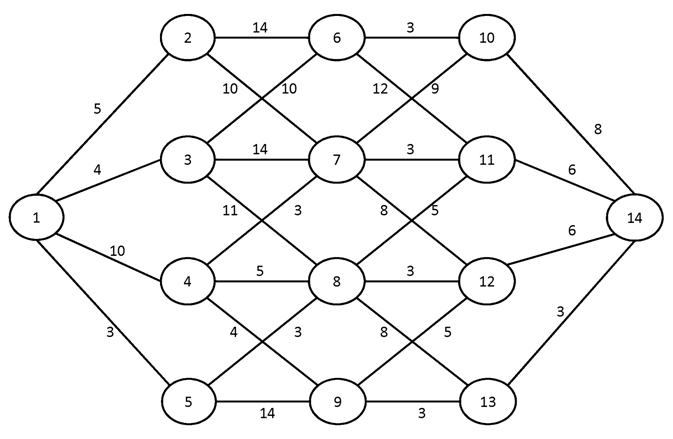
№3.
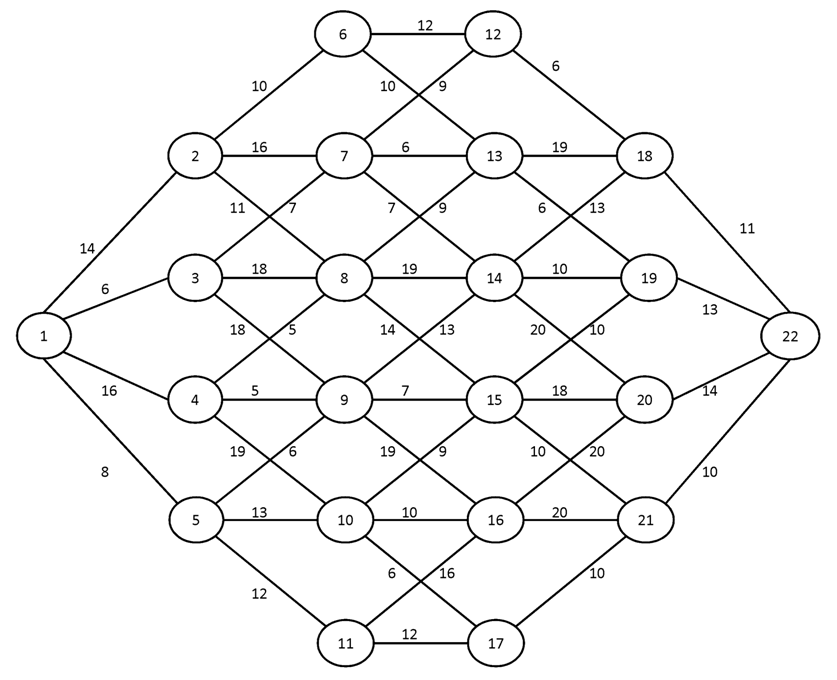
Вариант №3
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.
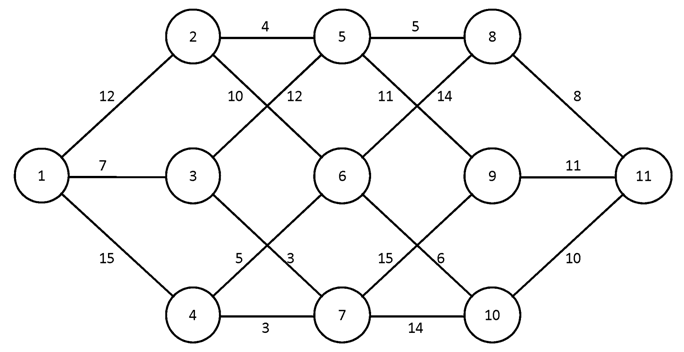
№2.
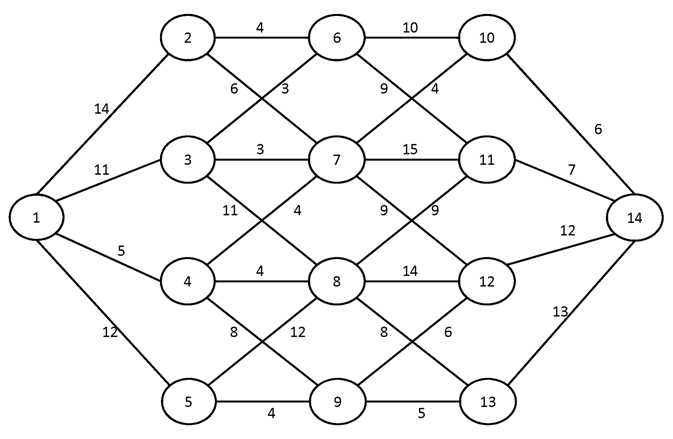
№3.
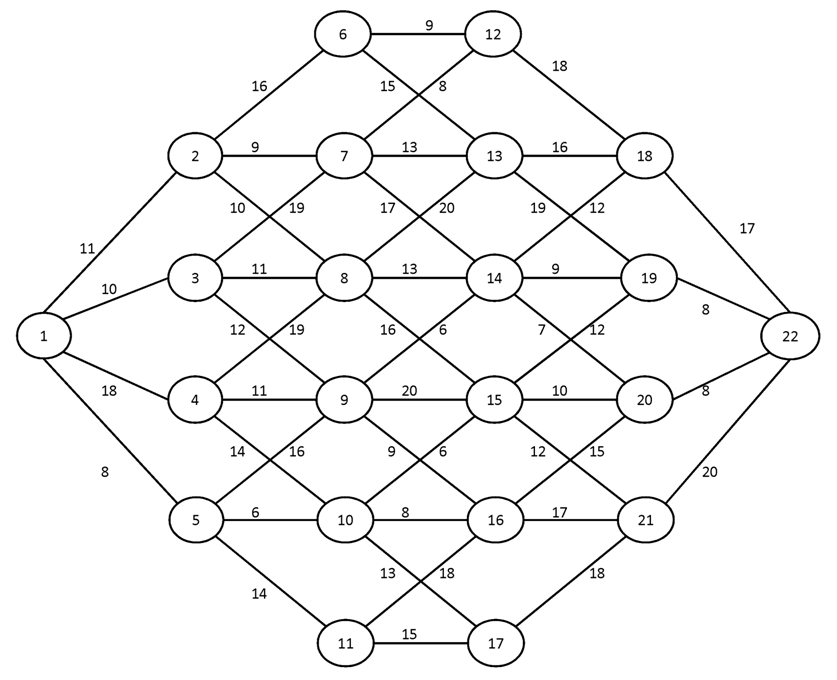
Вариант №4
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.
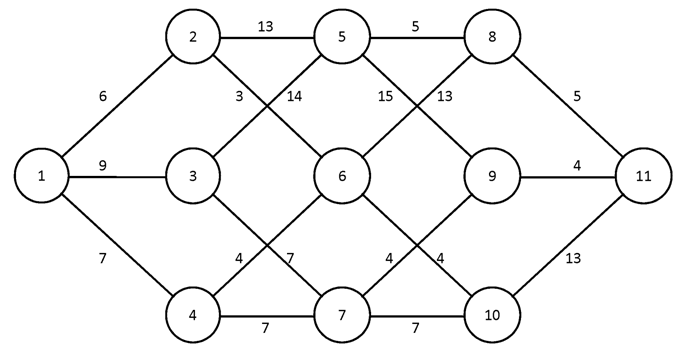
№2.
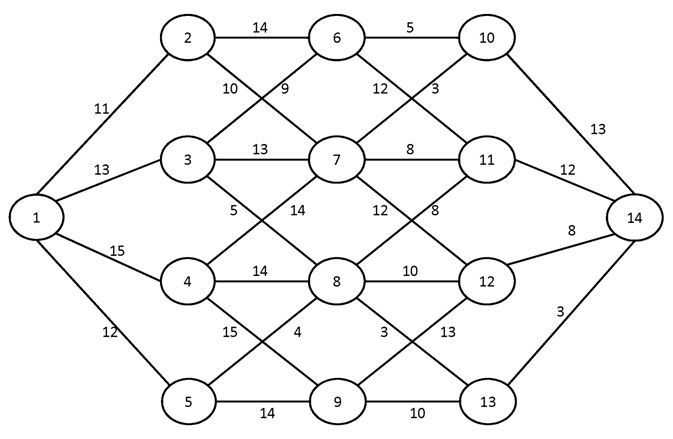
№3.
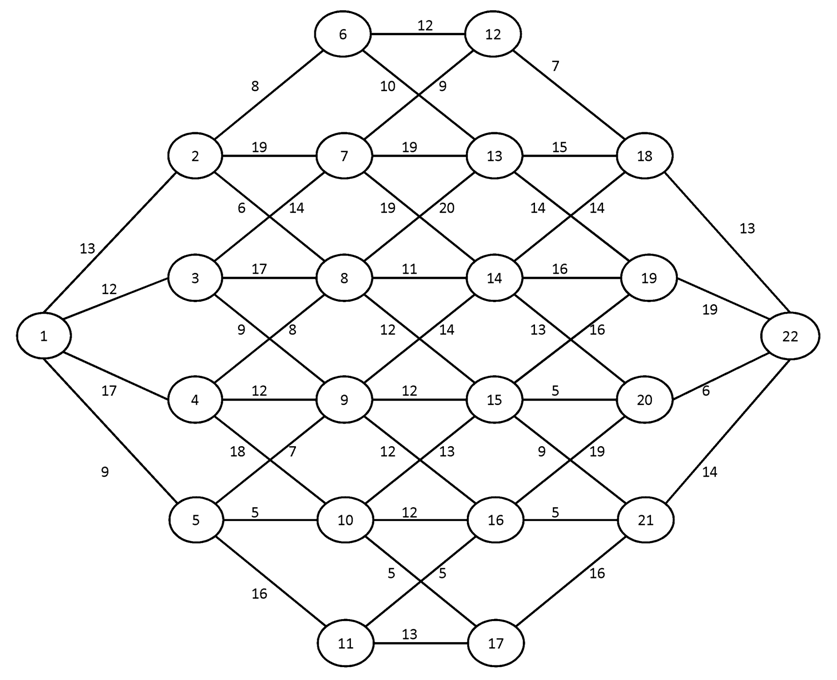
Вариант №5
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.
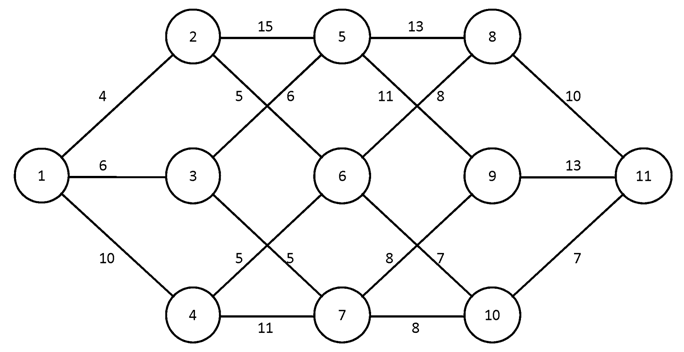
№2.
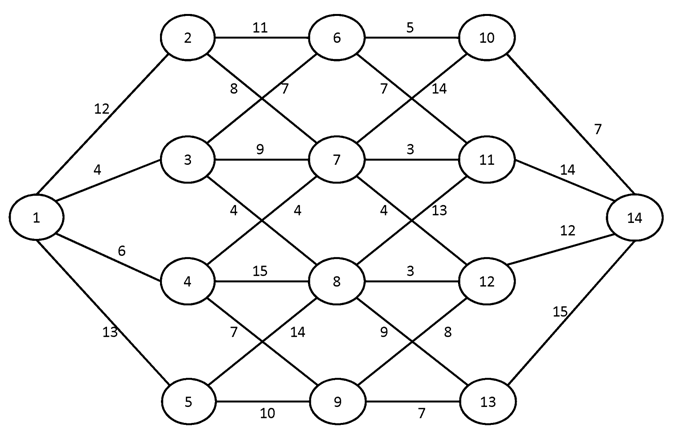
№3.
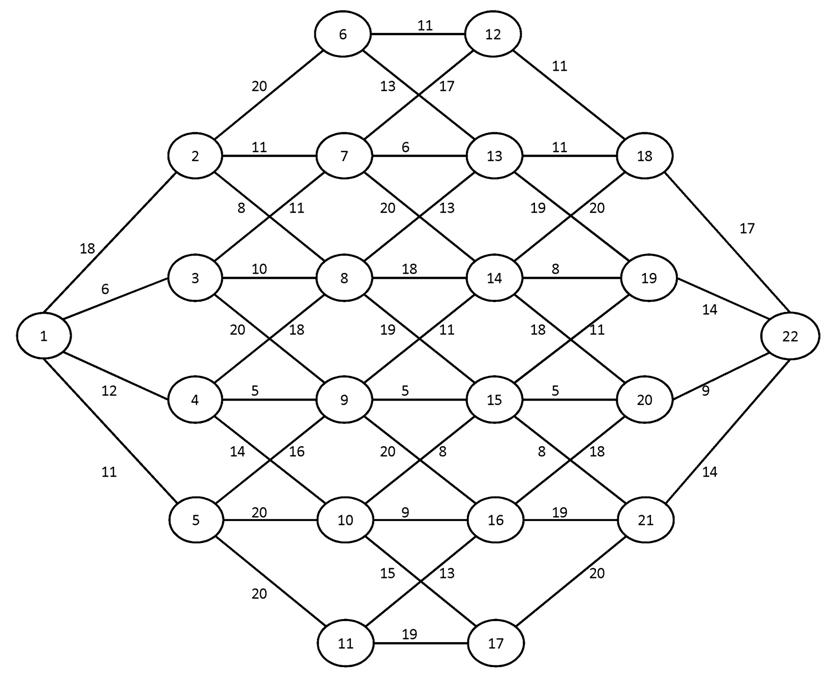
Вариант №6
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.
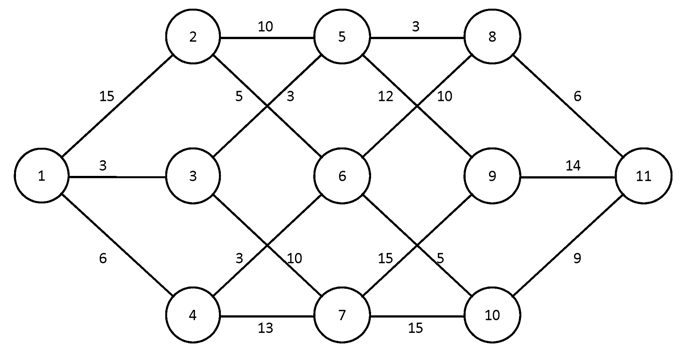
№2.
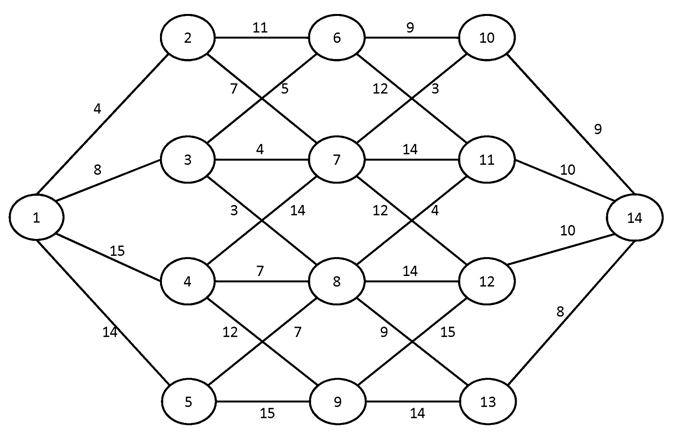
№3.

Вариант №7
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.

№2.
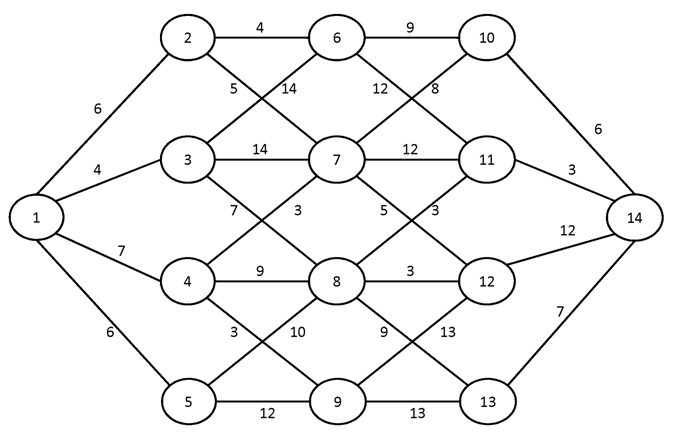
№3.
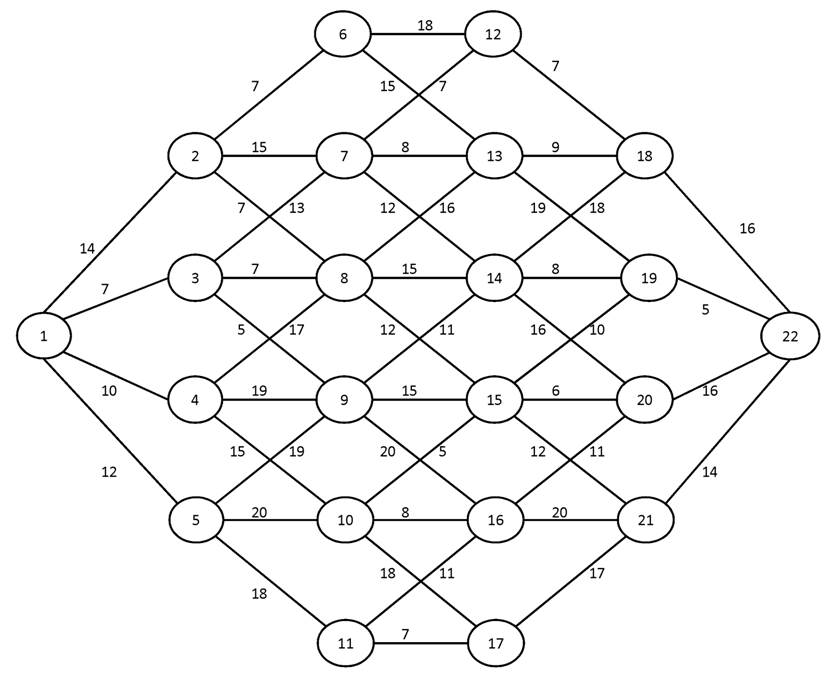
Вариант №8
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.
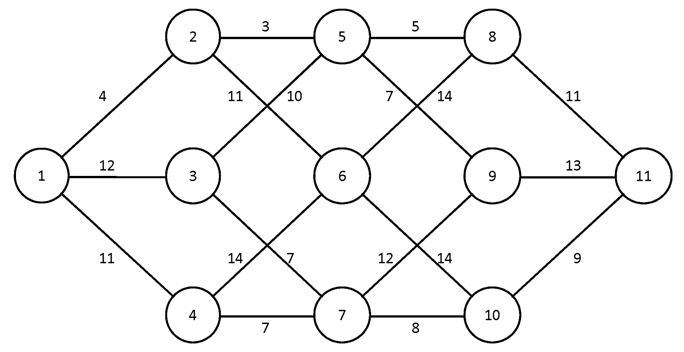
№2.
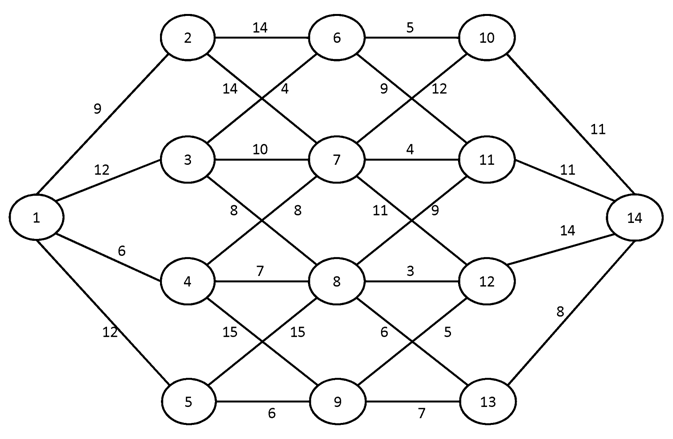
№3.
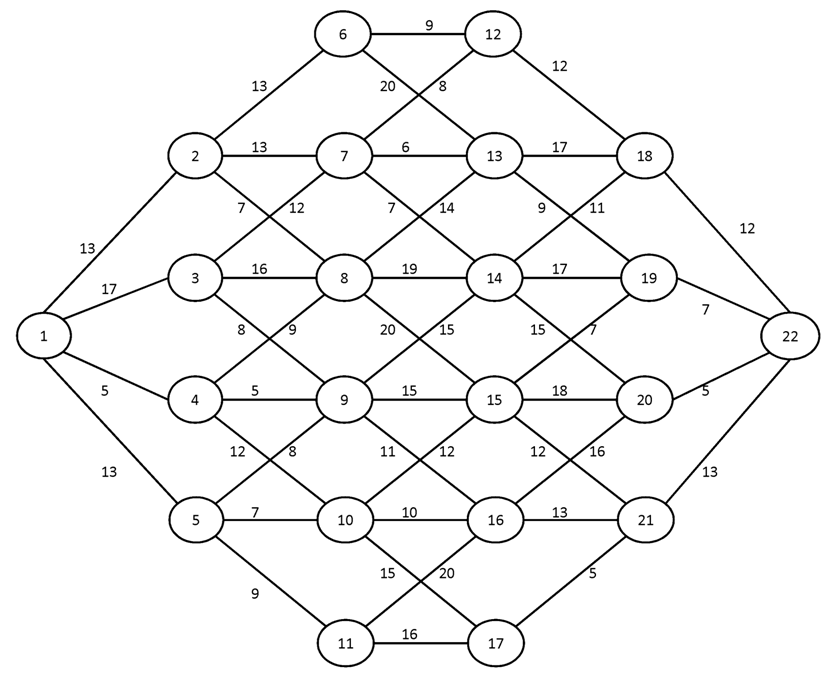
Вариант №9
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.
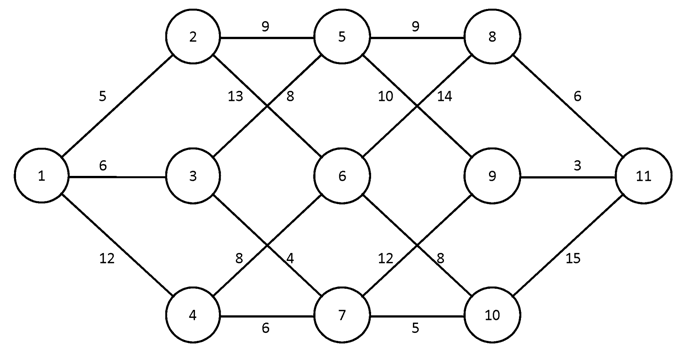
№2.
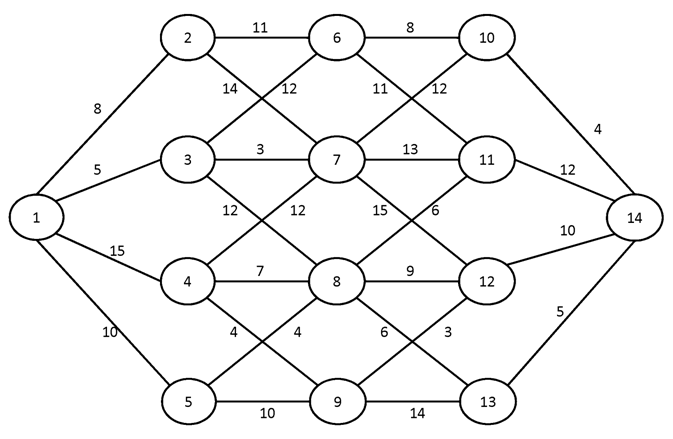
№3.
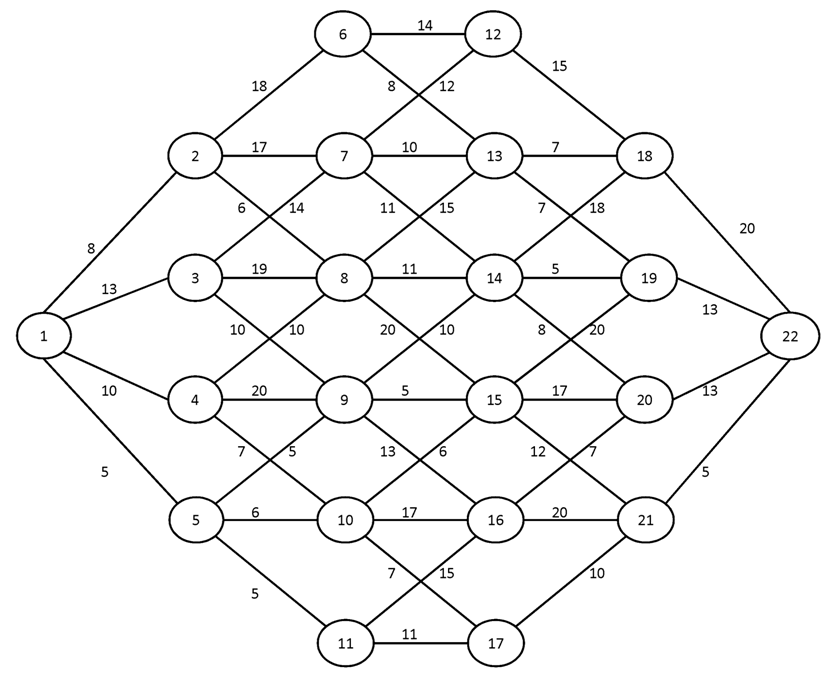
Вариант №10
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.
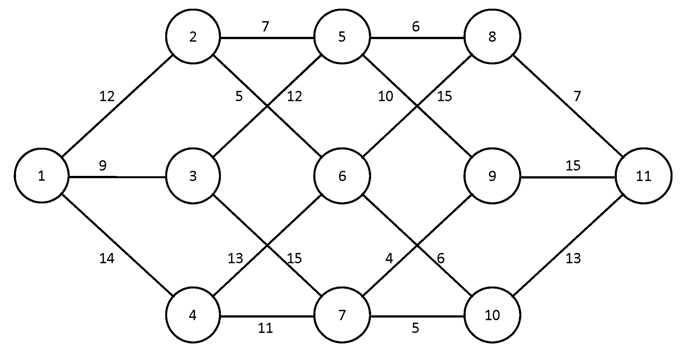
№2.

№3.
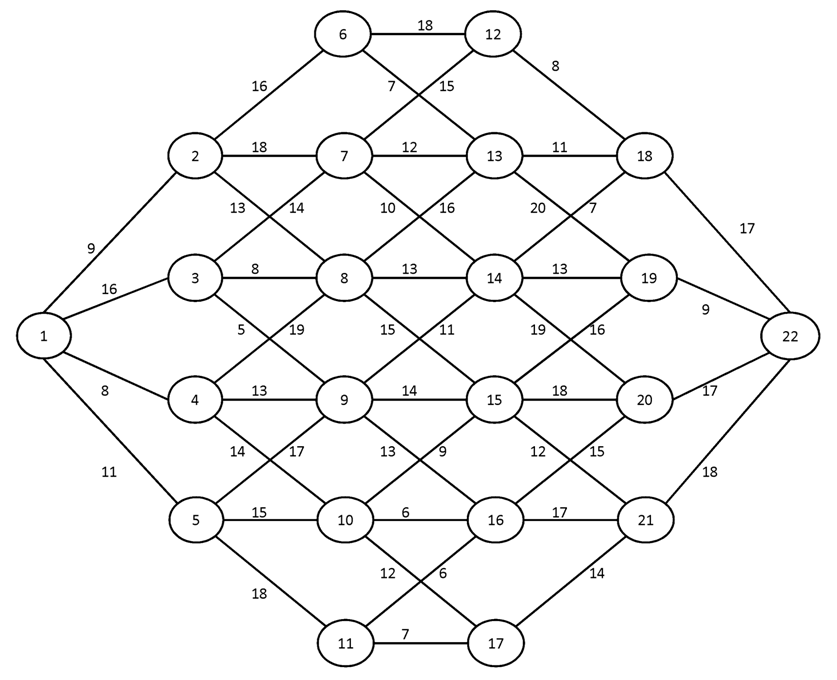
Вариант №11
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.
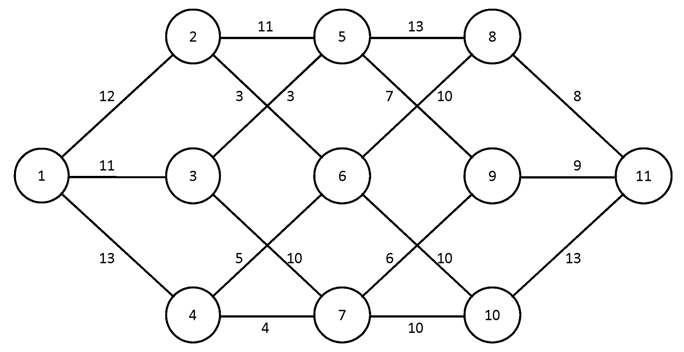
№2.
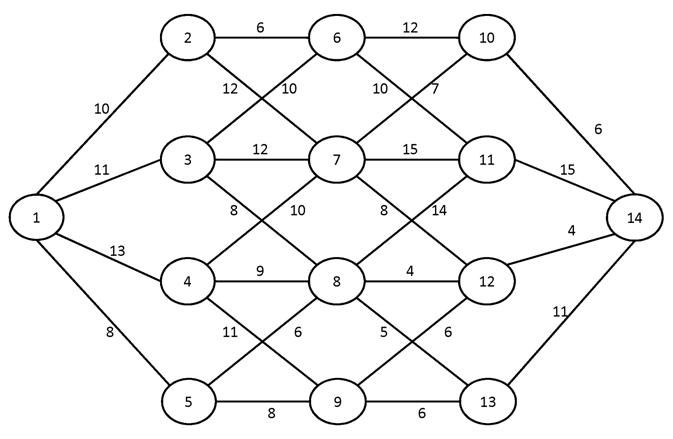
№3.
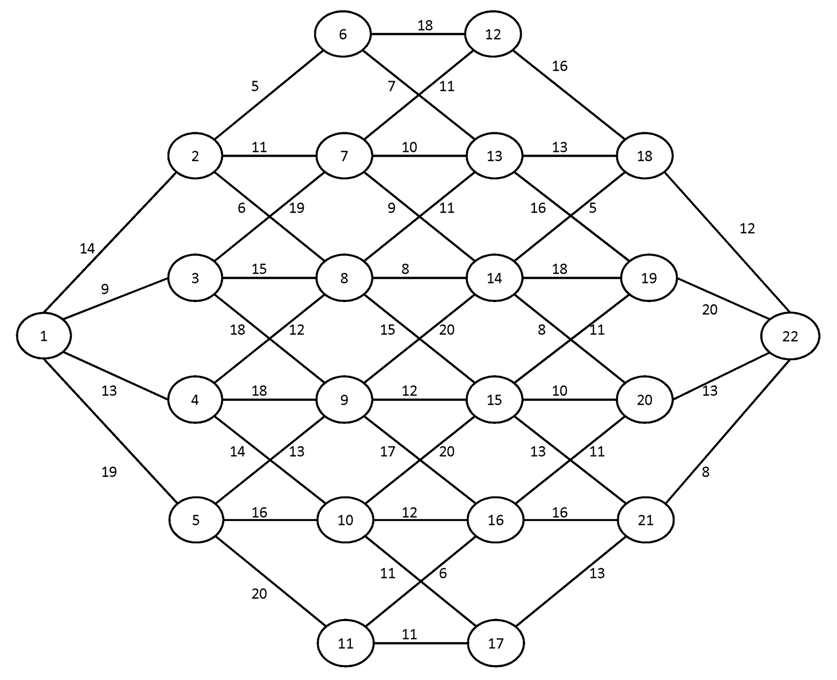
Вариант №12
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.
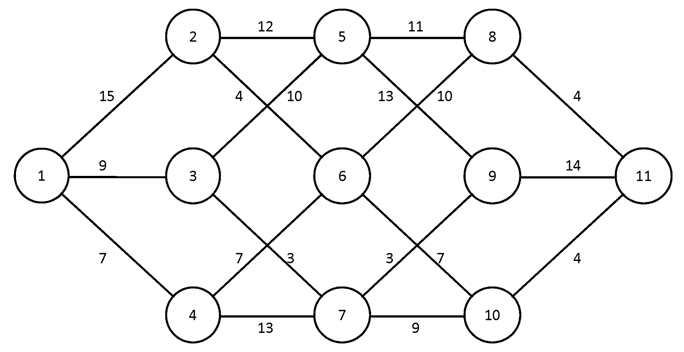
№2.

№3.
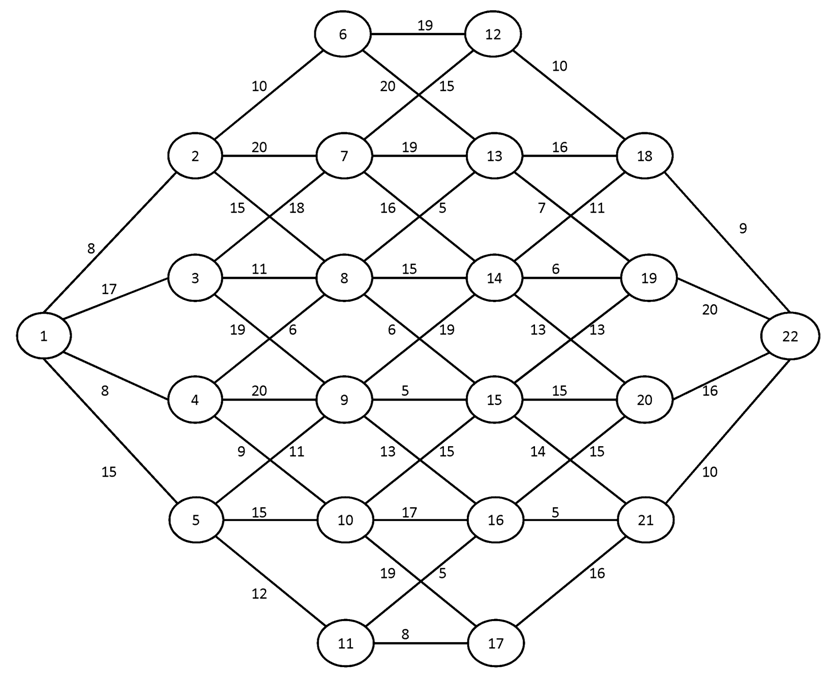
Вариант №13
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.
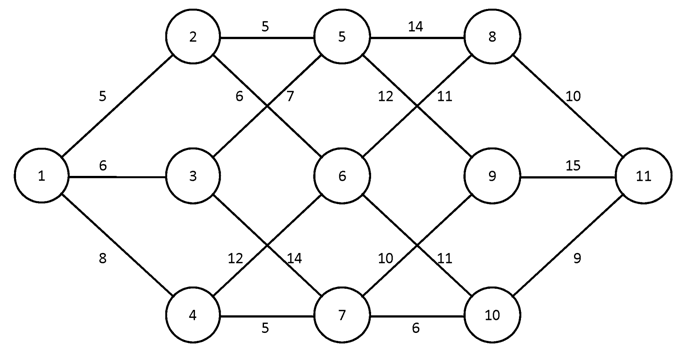
№2.
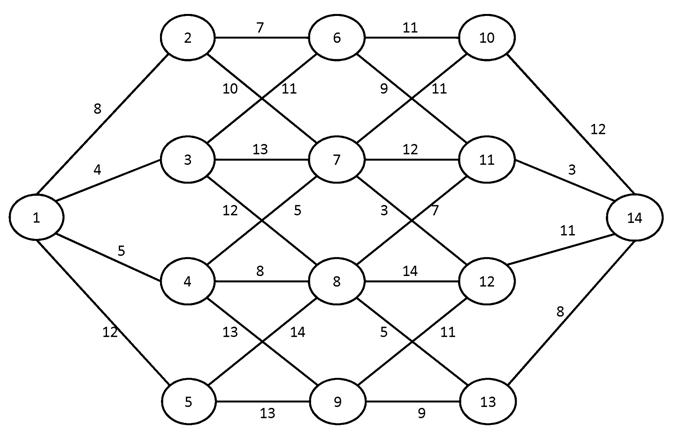
№3.
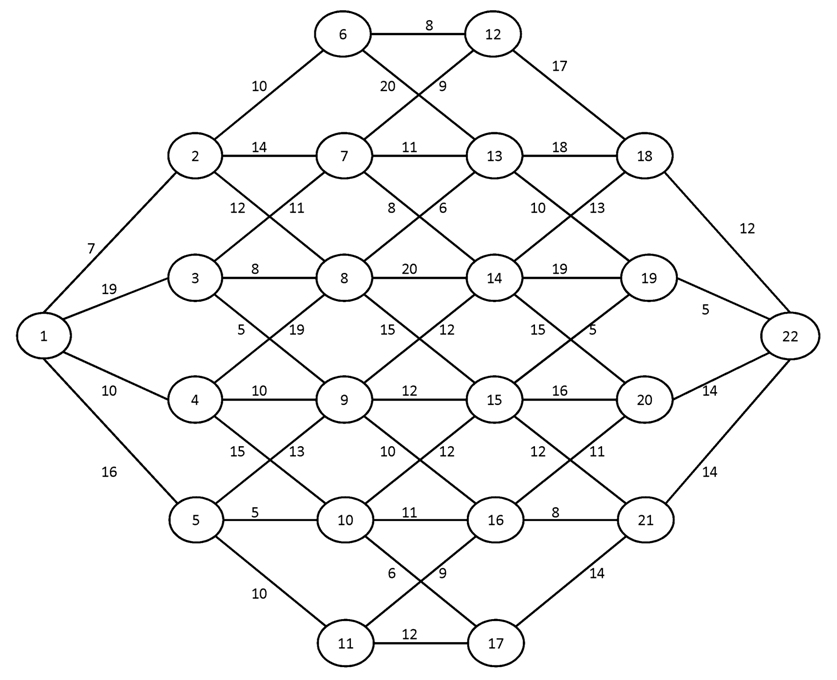
Вариант №14
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.
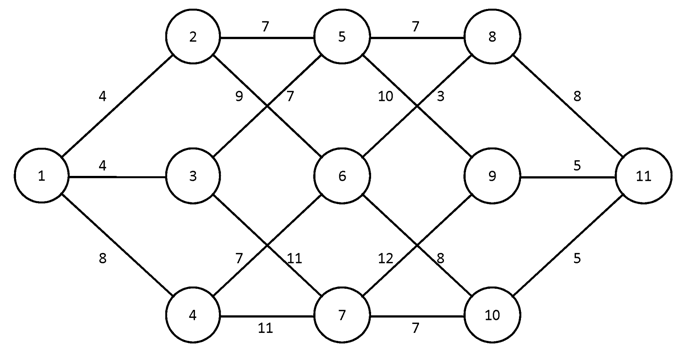
№2.
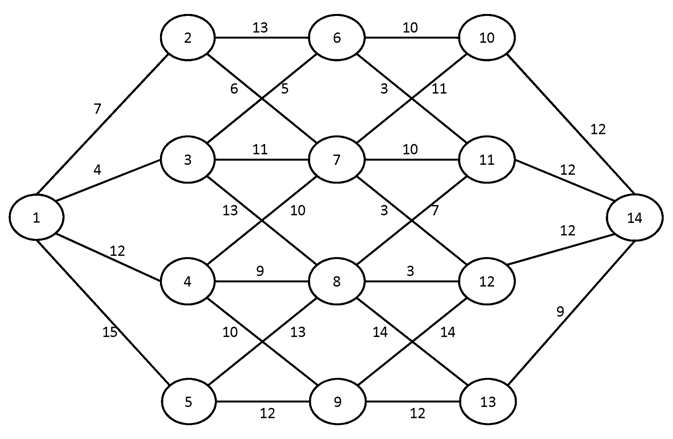
№3.
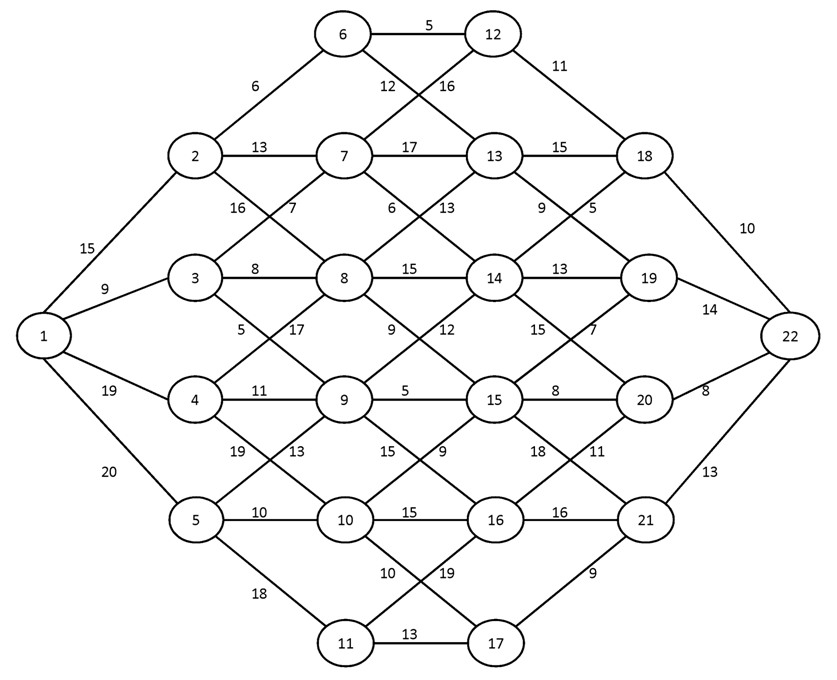
Вариант №15
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.
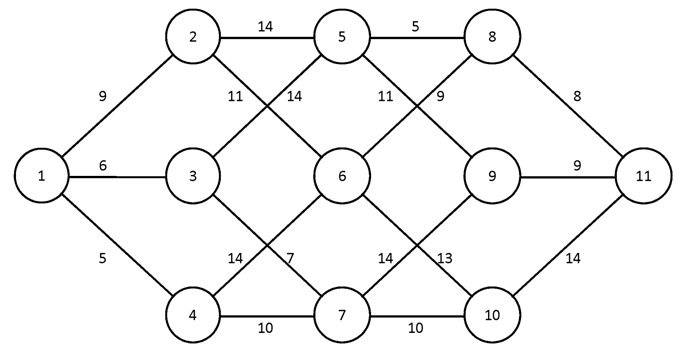
№2.
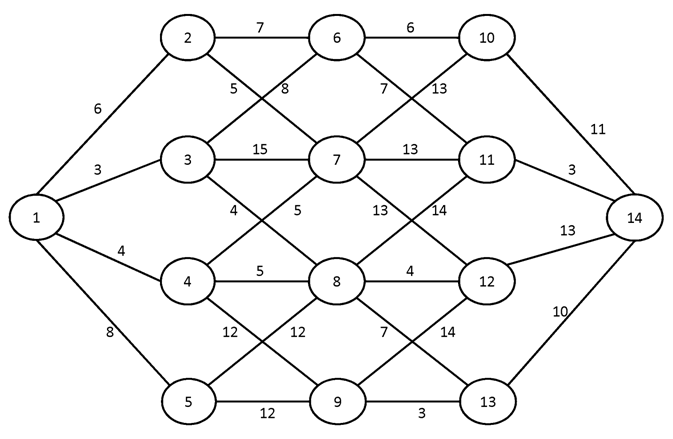
№3.
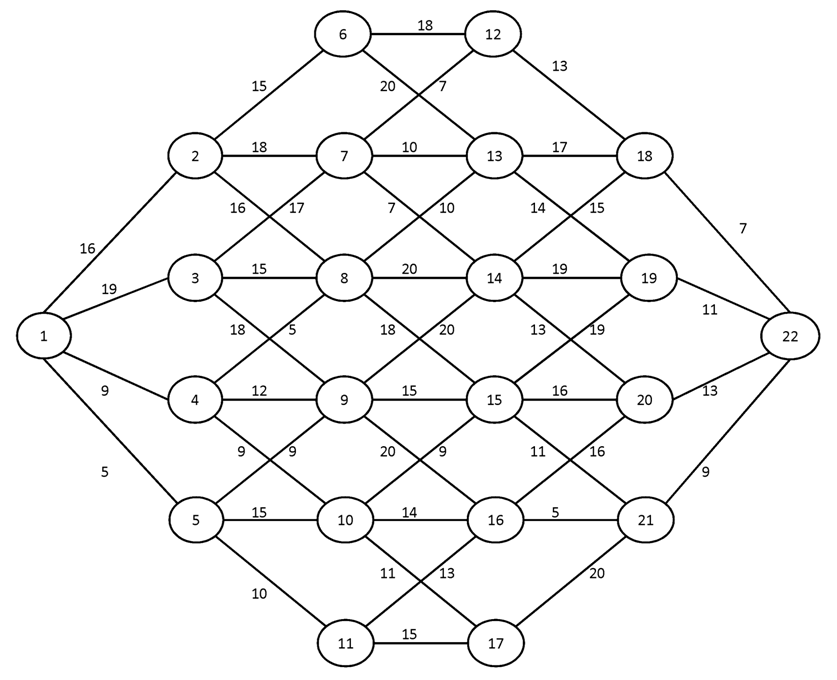
Вариант №16
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.
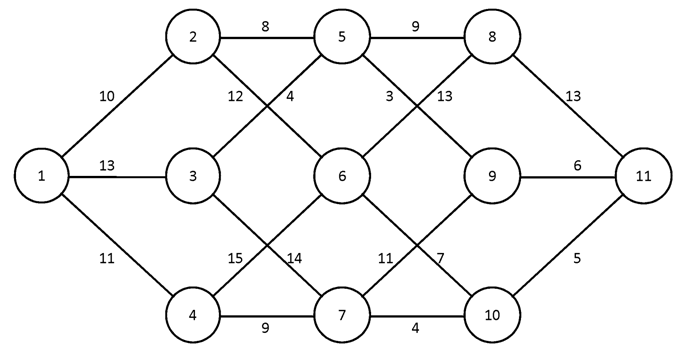
№2.

№3.
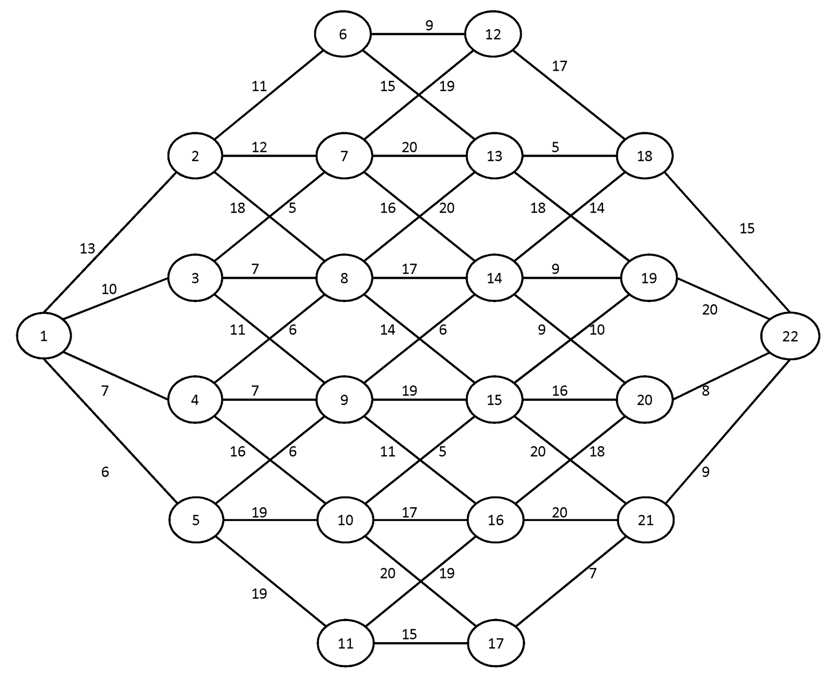
Вариант №17
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.
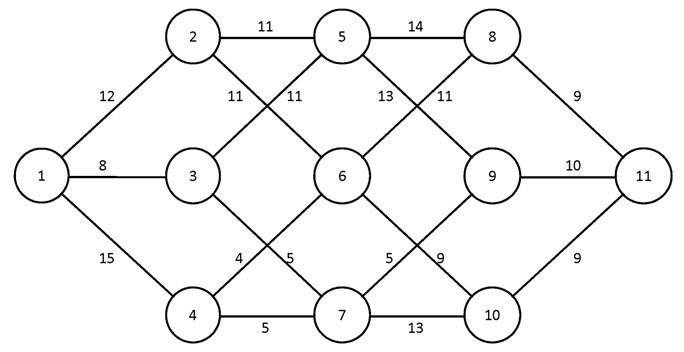
№2.
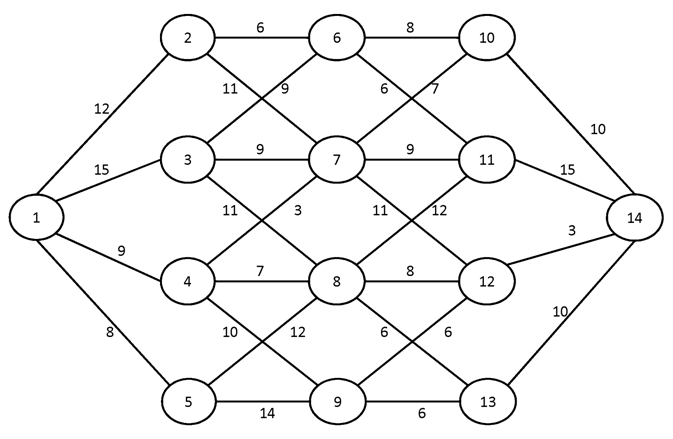
№3.
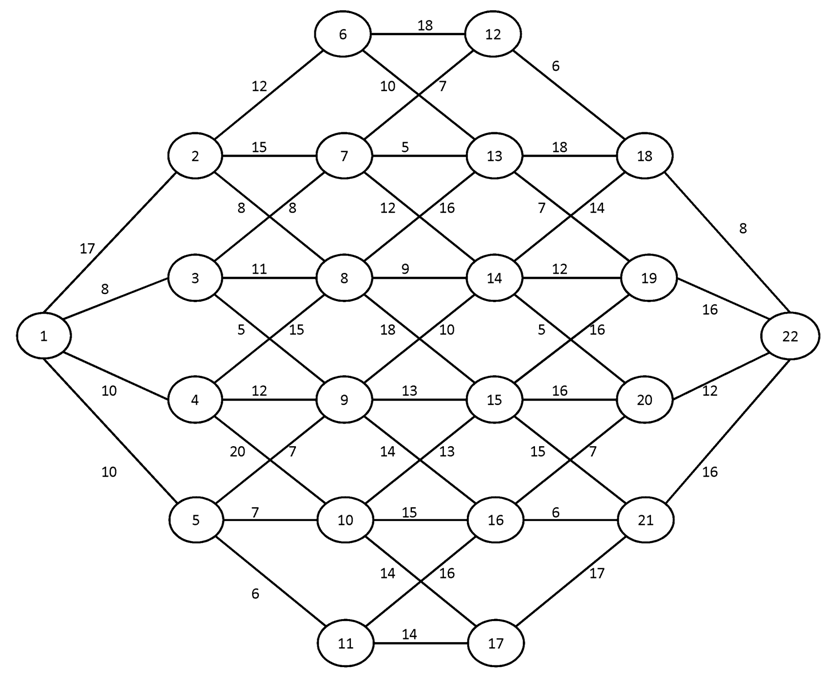
Вариант №18
Найти кратчайшие пути от вершины 1 ко всем остальным вершинам графа.
№1.
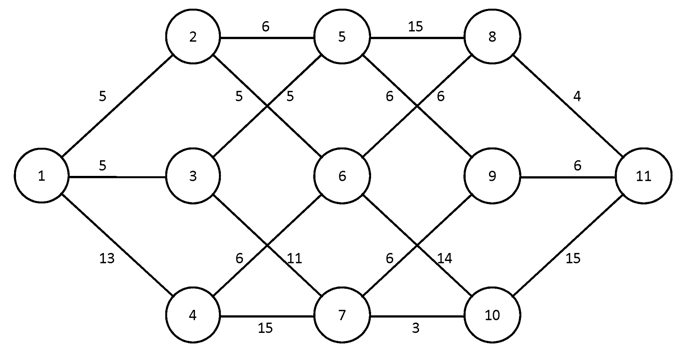
№2.
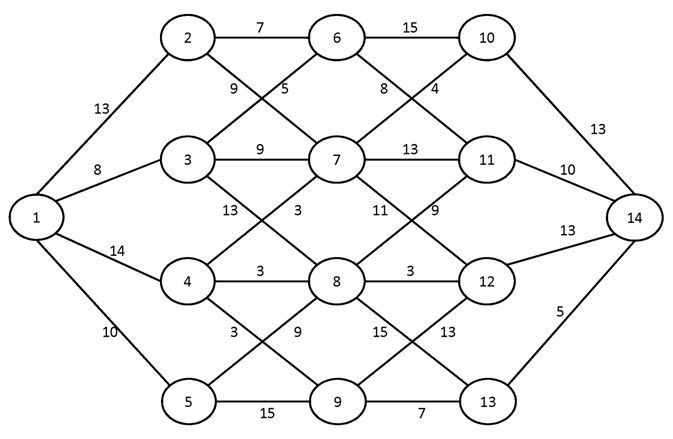
№3.
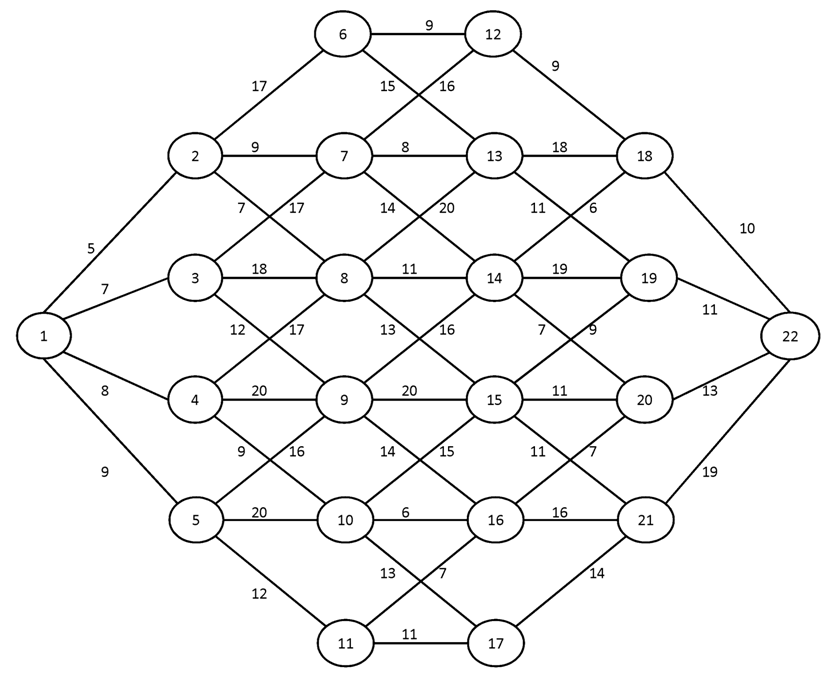
ВОПРОСЫ ВЫХОДНОГО КОНТРОЛЯ:
- Дайте определение графа, приведите примеры.
- Сформулируйте определение пути (маршрута).
- Дайте понятие кратчайшего пути.
- Сформулируйте постановку задачи нахождения кратчайшего пути от заданного узла до всех остальных узлов в графе.
- Объясните суть алгоритма Дейкстры.
ДОМАШНЕЕ ЗАДАНИЕ:
Выучить алгоритм Дейкстры.