ЭЛЕКТРОННЫЙ ЛАБОРАТОРНЫЙ ПРАКТИКУМ
ПО УЧЕБНОМУ ПРЕДМЕТУ
"ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ"
№13. Решение задачи нахождения кратчайших путей между всеми парами узлов с использованием алгоритма Флойда
Цель: научить находить кратчайшие цепи в графе при помощи алгоритма Флойда.
Оборудование: практикум, тетрадь для лабораторных и практических работ.
Литература:
- Кристофидес Н. Теория графов. Алгоритмический подход. - М.: Мир, 1979. С. 189-191.
- Новиков Ф. А. Дискретная математика для программистов. - СПб.: Питер, 2000. С. 228-232.
- Таха, Хемди. Введение в исследование операций - М.: Издательский дом "Вильямс", 2005. С. 250-265.
Время выполнения: 2 часа.
ВОПРОСЫ ВХОДНОГО КОНТРОЛЯ:
- Дайте определение графа, приведите примеры.
- Сформулируйте определение пути (маршрута).
- Дайте понятие кратчайшего пути.
- Сформулируйте постановку задачи нахождения кратчайшего пути от заданного узла до всех остальных узлов в графе.
- Объясните суть алгоритма Флойда.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:
Алгоритм Флойда находит кратчайшие пути между любыми двумя узлами сети. В этом алгоритме сеть представлена в виде квадратной матрицы с n строками и n столбцами. Элемент (i, j) равен расстоянию dij от узла i к узлу j, которое имеет конечное значение, если существует дуга (i, j), и равен бесконечности в противном случае.
Основная идея метода Флойда: пусть есть три узла i, j и k и заданы расстояния между ними. Если выполняется неравенство dij + djk < dik, то целесообразно заменить путь i → k путем i → j → k. Такая замена (далее ее будем условно называть треугольным оператором) выполняется систематически в процессе выполнения алгоритма Флойда.
Алгоритм Флойда
1) Определяем начальную матрицу расстояний D0 и матрицу последовательности узлов S0. Диагональные элементы обеих матриц помечаются знаком "-", показывающим, что эти элементы в вычислениях не участвуют. Полагаем k = 1;
2) Задаем строку k и столбец k как разрешающую строку и разрешающий столбец. Рассматриваем возможность применения треугольного оператора ко всем элементам dij матрицы Dk-1. Если выполняется неравенство
dik + dkj < dij (i ≠ k, j ≠ k, i ≠ j),
то делаем следующее:
a) создаем матрицу Dk путем замены в матрице Dk-1 элемента dij суммой dik + dkj,
b) создаем матрицу Sk, меняя в матрице Sk-1 элемент sij на k.
3) Полагаем k = k + 1, повторяем этап 2 до тех пор, пока выполняется условие k ≤ n.
4) После реализации n этапов алгоритма определение по матрицам Dn и Sn кратчайшего пути между узлами i и j выполняется по следующим правилам:
а) расстояние между узлами i и j равно элементу dij в матрице Dn;
б) промежуточные узлы пути от узла i к узлу j определяем по матрице Sn. Пусть sij = k, тогда имеем путь i → k → j. Если далее sik = k и skj = j, тогда считаем, что весь путь определен, так как найдены все промежуточные узлы. В противном случае повторяем описанную процедуру для путей от узла i к узлу k и от узла k к узлу j.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ:
Найти кратчайшие пути между всеми парами вершин графа

СОДЕРЖАНИЕ РАБОТЫ:
Вариант №1
Найти кратчайшие пути между всеми парами вершин графа.
№1.
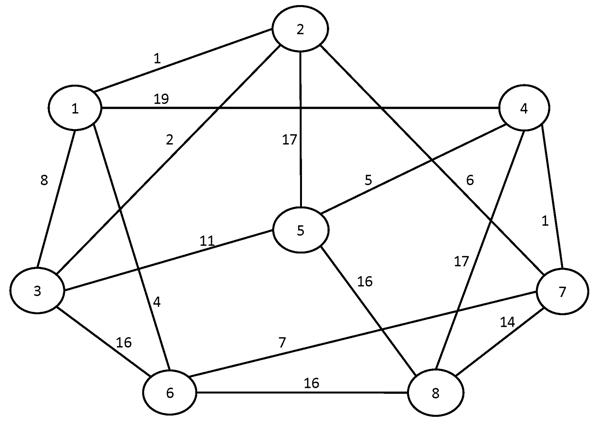
№2.
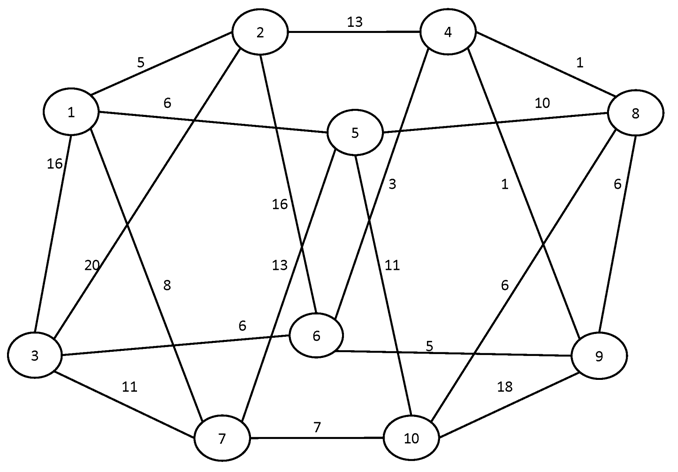
Вариант №2
Найти кратчайшие пути между всеми парами вершин графа.
№1.

№2.
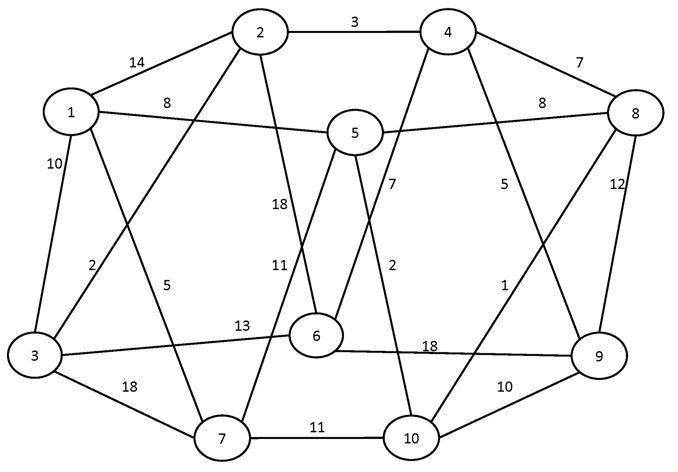
Вариант №3
Найти кратчайшие пути между всеми парами вершин графа.
№1.
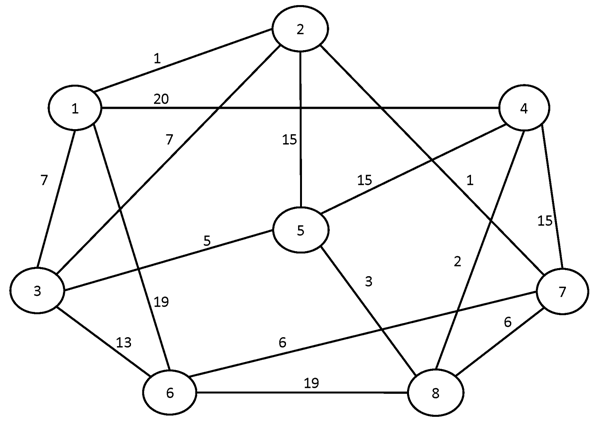
№2.
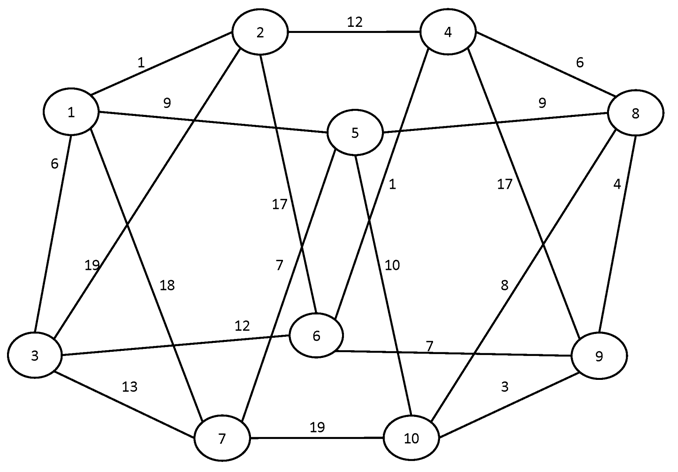
Вариант №4
Найти кратчайшие пути между всеми парами вершин графа.
№1.
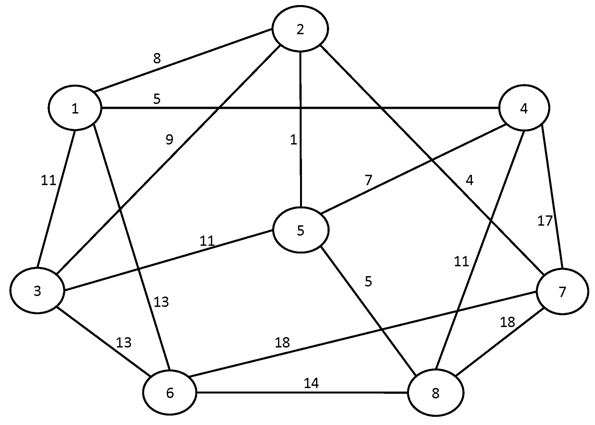
№2.
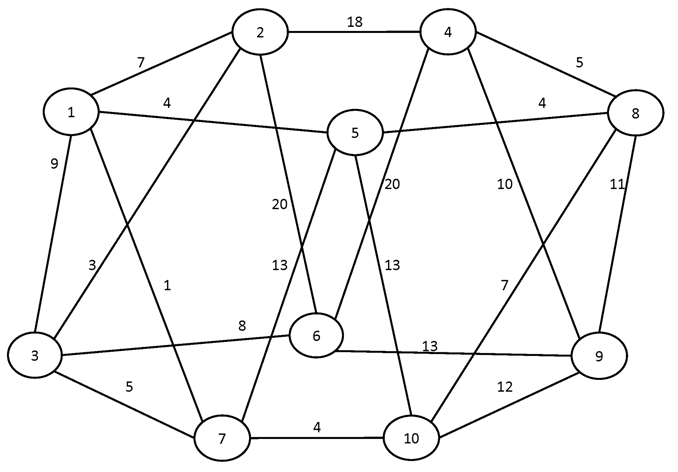
Вариант №5
Найти кратчайшие пути между всеми парами вершин графа.
№1.
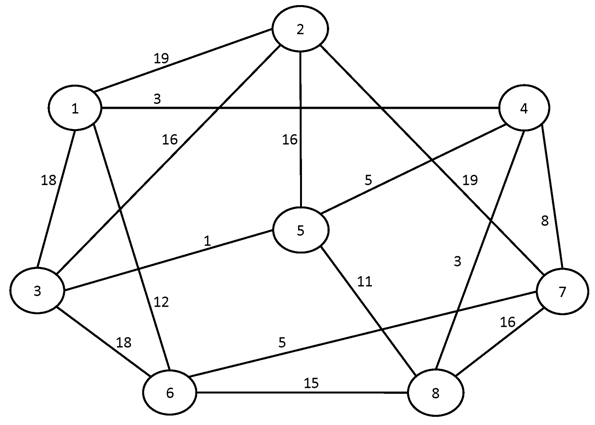
№2.
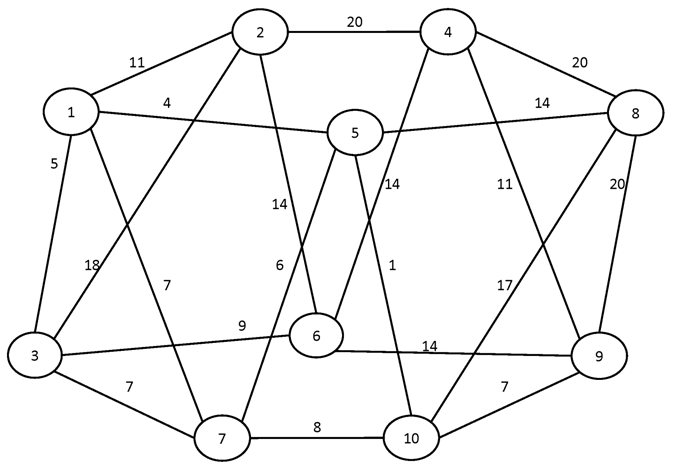
Вариант №6
Найти кратчайшие пути между всеми парами вершин графа.
№1.
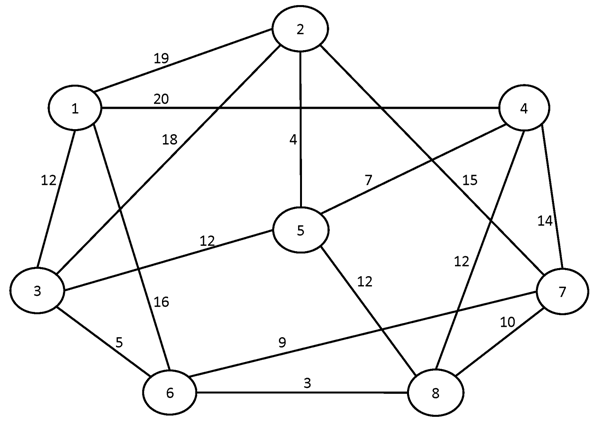
№2.
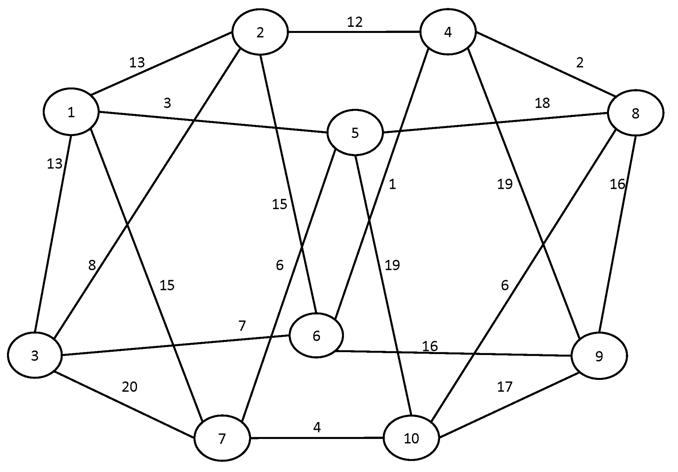
Вариант №7
Найти кратчайшие пути между всеми парами вершин графа.
№1.

№2.
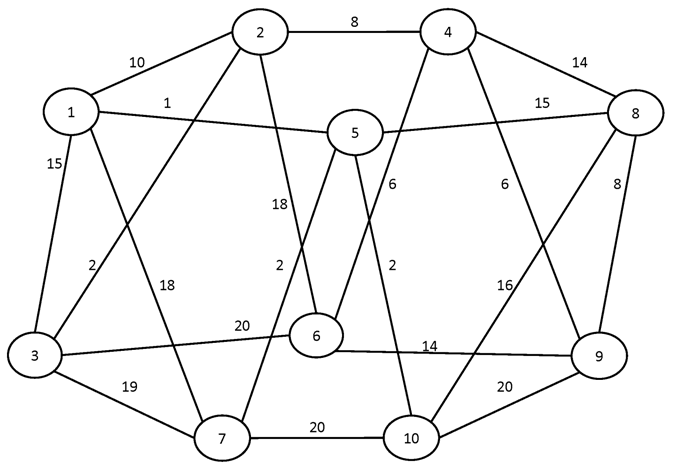
Вариант №8
Найти кратчайшие пути между всеми парами вершин графа.
№1.

№2.

Вариант №9
Найти кратчайшие пути между всеми парами вершин графа.
№1.
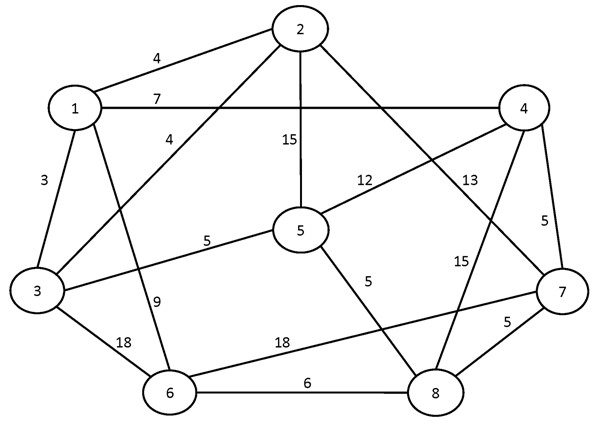
№2.

Вариант №10
Найти кратчайшие пути между всеми парами вершин графа.
№1.
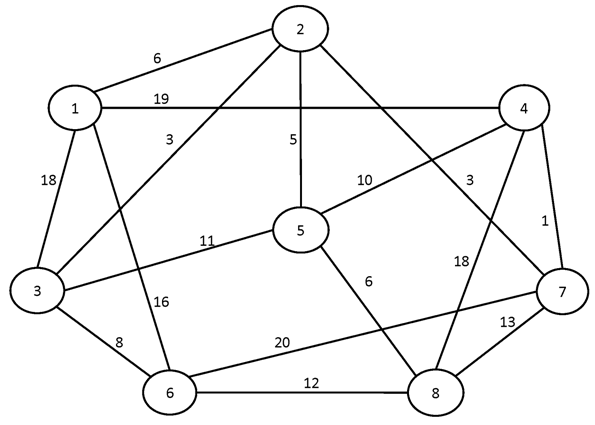
№2.

Вариант №11
Найти кратчайшие пути между всеми парами вершин графа.
№1.
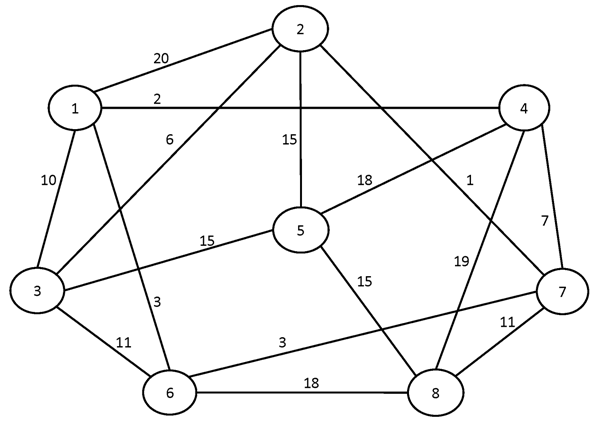
№2.
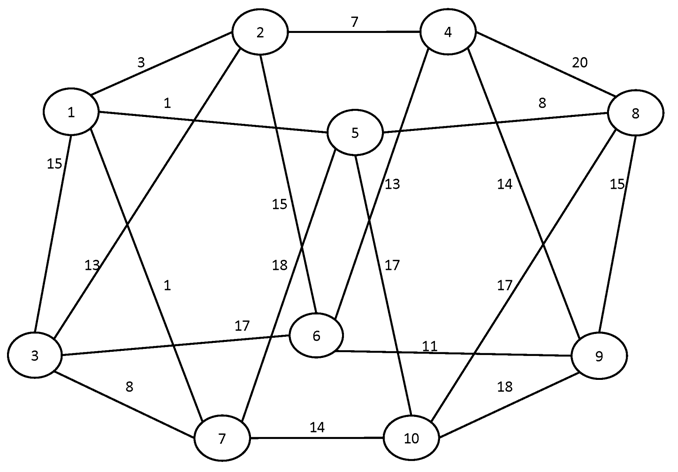
Вариант №12
Найти кратчайшие пути между всеми парами вершин графа.
№1.
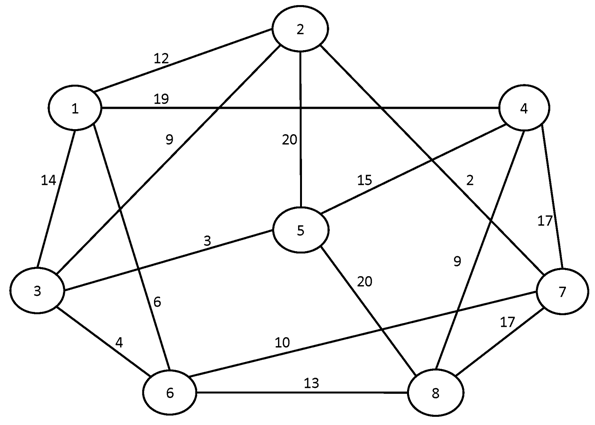
№2.
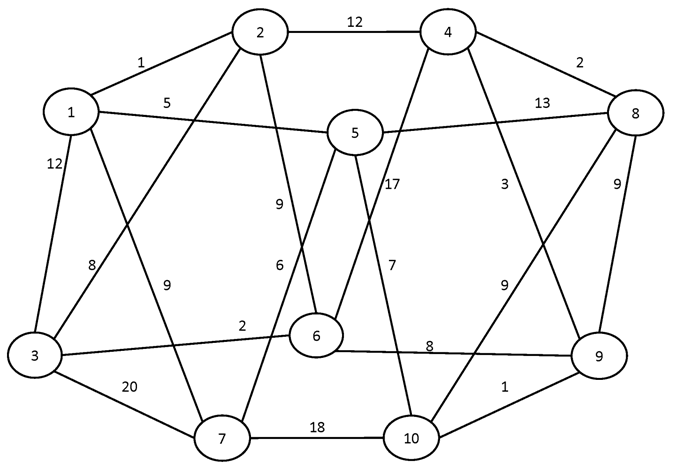
Вариант №13
Найти кратчайшие пути между всеми парами вершин графа.
№1.
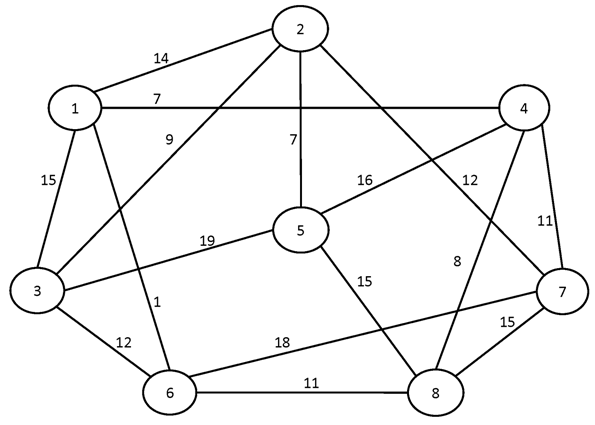
№2.

Вариант №14
Найти кратчайшие пути между всеми парами вершин графа.
№1.
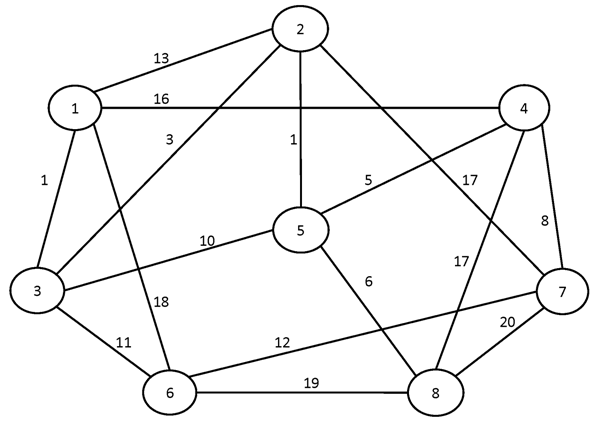
№2.
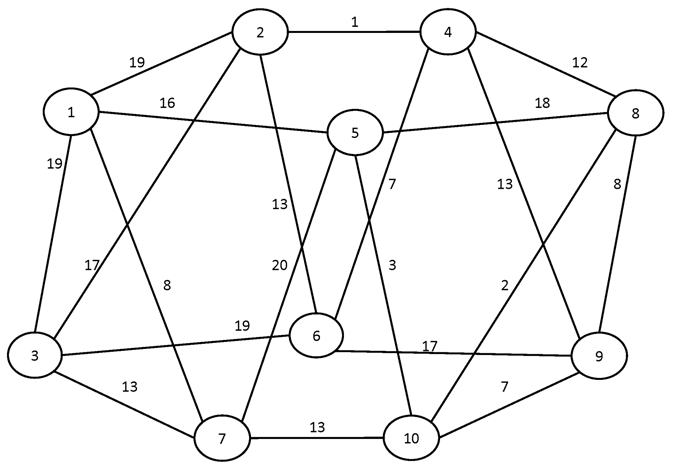
Вариант №15
Найти кратчайшие пути между всеми парами вершин графа.
№1.
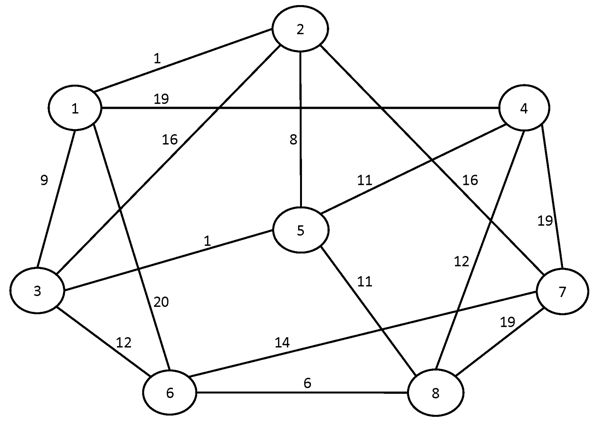
№2.
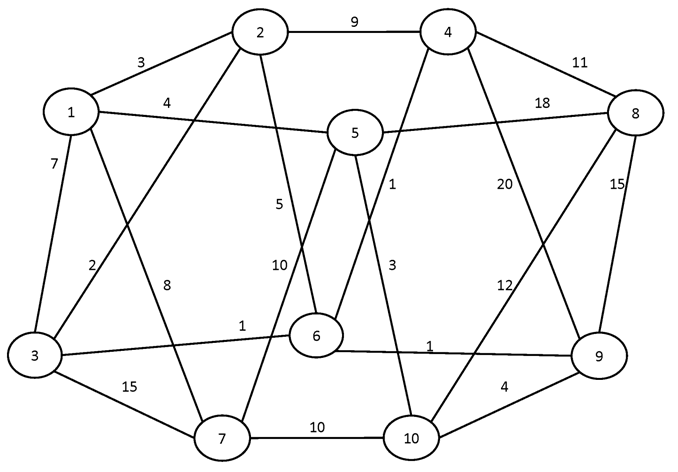
Вариант №16
Найти кратчайшие пути между всеми парами вершин графа.
№1.
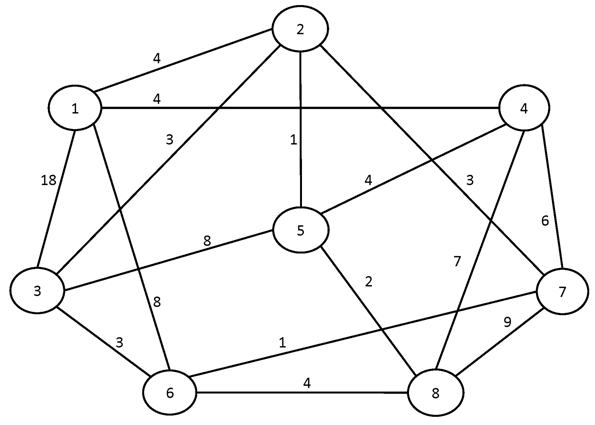
№2.

Вариант №17
Найти кратчайшие пути между всеми парами вершин графа.
№1.

№2.

Вариант №18
Найти кратчайшие пути между всеми парами вершин графа.
№1.

№2.
ВОПРОСЫ ВЫХОДНОГО КОНТРОЛЯ:
- Дайте определение графа, приведите примеры.
- Сформулируйте определение пути (маршрута).
- Дайте понятие кратчайшего пути.
- Сформулируйте постановку задачи нахождения кратчайшего пути от заданного узла до всех остальных узлов в графе.
- Объясните суть алгоритма Флойда.
ДОМАШНЕЕ ЗАДАНИЕ:
Выучить алгоритм Флойда.