ЭЛЕКТРОННЫЙ ЛАБОРАТОРНЫЙ ПРАКТИКУМ
ПО УЧЕБНОМУ ПРЕДМЕТУ
"ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ"
№14. Решение задачи нахождения максимального потока в сети с использованием алгоритма Форда–Фалкерсона
Цель: научить находить максимальный поток и строить минимальный разрез в сети.
Оборудование: практикум, тетрадь для лабораторных и практических работ.
Литература:
- Кристофидес Н. Теория графов. Алгоритмический подход. - М.: Мир, 1979. С. 310-329.
- Новиков Ф. А. Дискретная математика для программистов. - СПб.: Питер, 2000. С. 220-226.
- Таха, Хемди. Введение в исследование операций - М.: Издательский дом "Вильямс", 2005. С. 269-283.
Время выполнения: 2 часа.
ВОПРОСЫ ВХОДНОГО КОНТРОЛЯ:
- Дайте определение графа, приведите примеры.
- Объясните понятие сети.
- Сформулируйте определение разреза.
- Сформулируйте определение потока.
- Сформулируйте определение максимального потока.
- Объясните суть алгоритма Форда-Фалкерсона.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:
Теорема Форда - Фалкерсона. На любой сети максимальная величина потока из истока I в сток S равна минимальной пропускной способности разреза, отделяющего I от S.
Алгоритм Форда - Фалкерсона
1) Построить некоторый начальный поток;
2) Организовать процедуру составления подмножества А вершин, достижимых из истока I по ненасыщенным ребрам. Если в этом процессе сток S не попадет в подмножество А, то построенный поток максимальный и задача решена. Если же S попал в A, то перейти к следующему этапу алгоритма.
3) Выделить путь из I в S, состоящий из ненасыщенных ребер, и увеличить поток хij по каждому ребру этого пути на величину Δ = min (rij - xij), где минимум берется по ребрам (i, j) упомянутого пути. Тем самым будет построен новый поток X1={x1ij}. После этого надо возвратиться к этапу 2 алгоритма.
При выполнении этапа 3 на каждом шаге по крайней мере одно из ненасыщенных ранее ребер становится насыщенным (именно то, которое соответствует Δ), а поскольку число ребер в сети конечно, через конечное число шагов максимальный поток будет построен.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ:
Найти максимальный поток в сети между истоком I = 1 и стоком S = 8.

Решение.
СОДЕРЖАНИЕ РАБОТЫ:
Вариант №1
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8
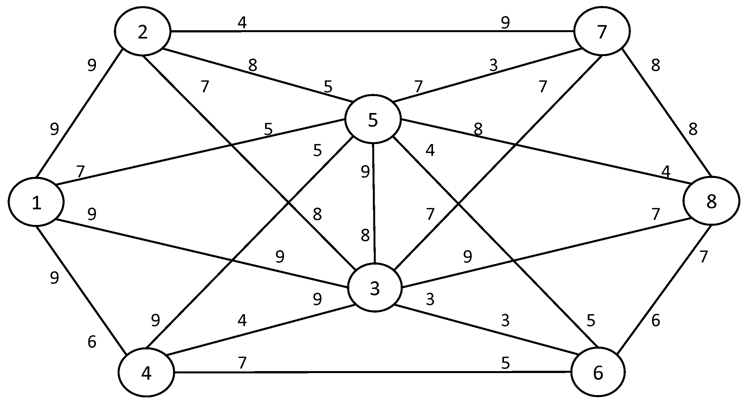
№2. I = 1 S = 10
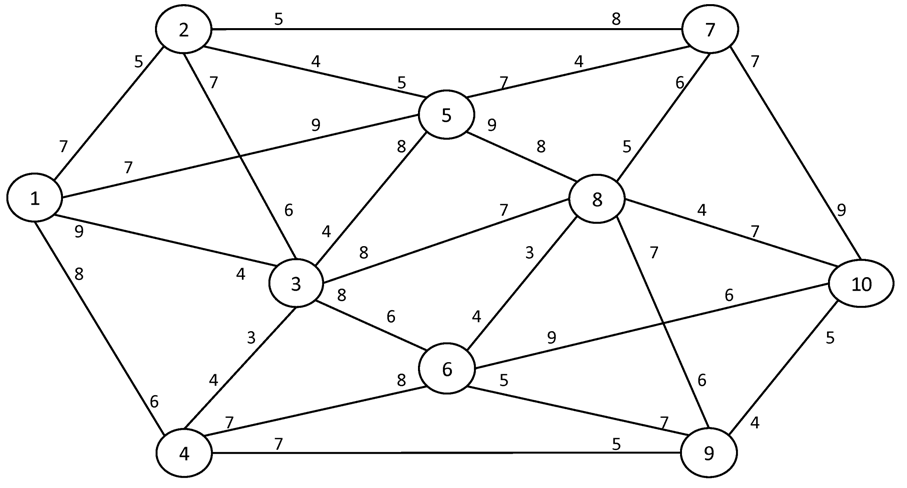
Вариант №2
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8
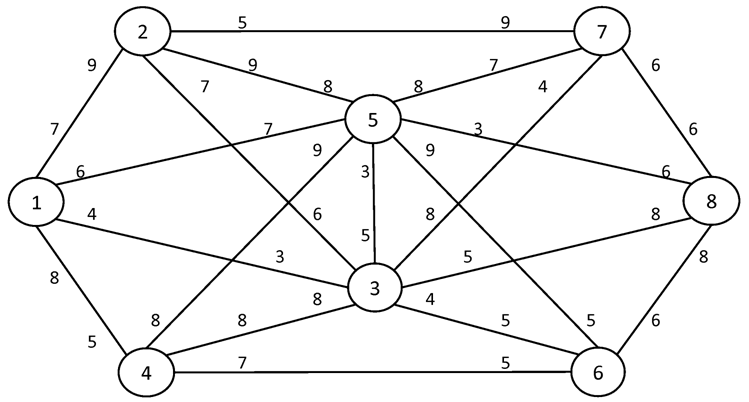
№2. I = 1 S = 10
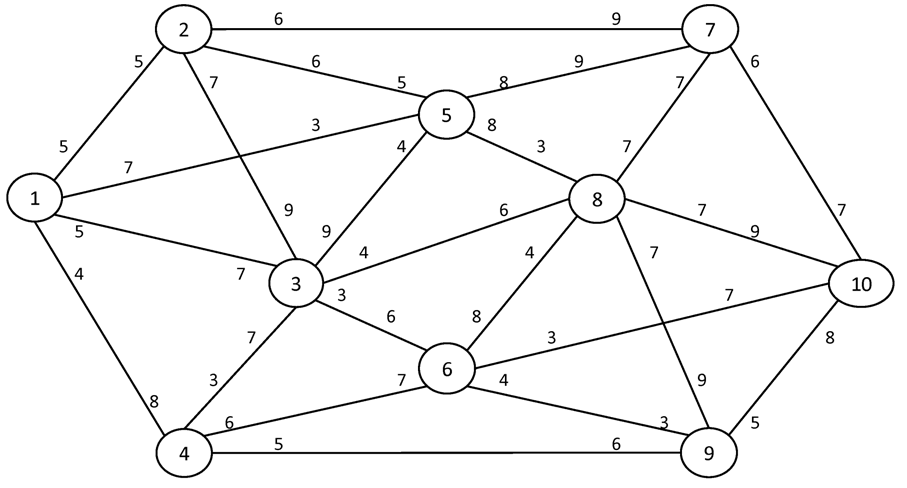
Вариант №3
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8
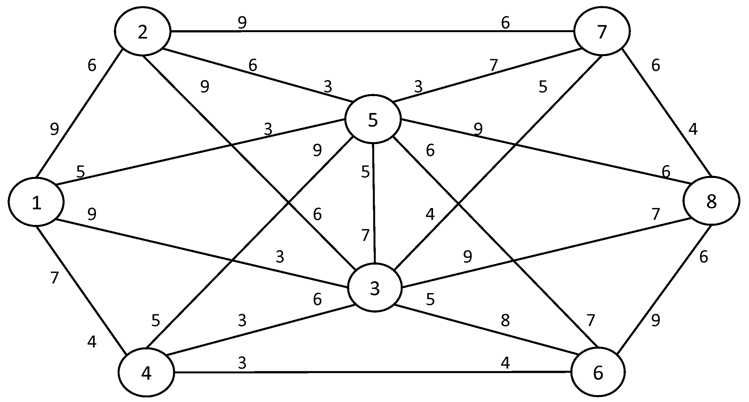
№2. I = 1 S = 10
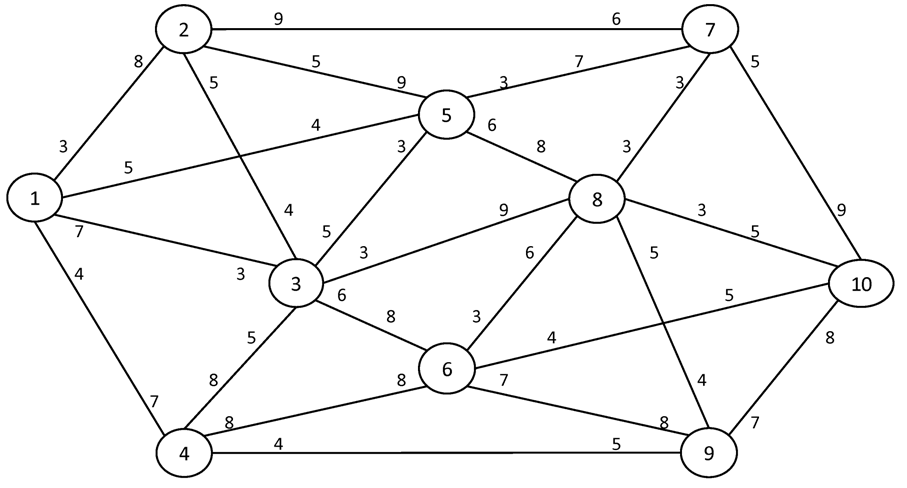
Вариант №4
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8

№2. I = 1 S = 10

Вариант №5
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8
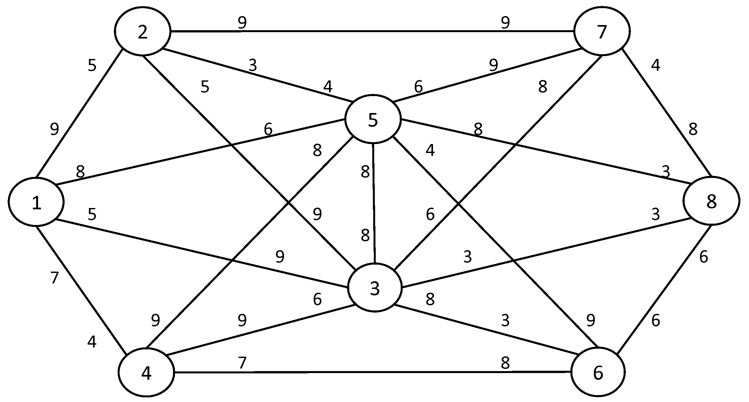
№2. I = 1 S = 10
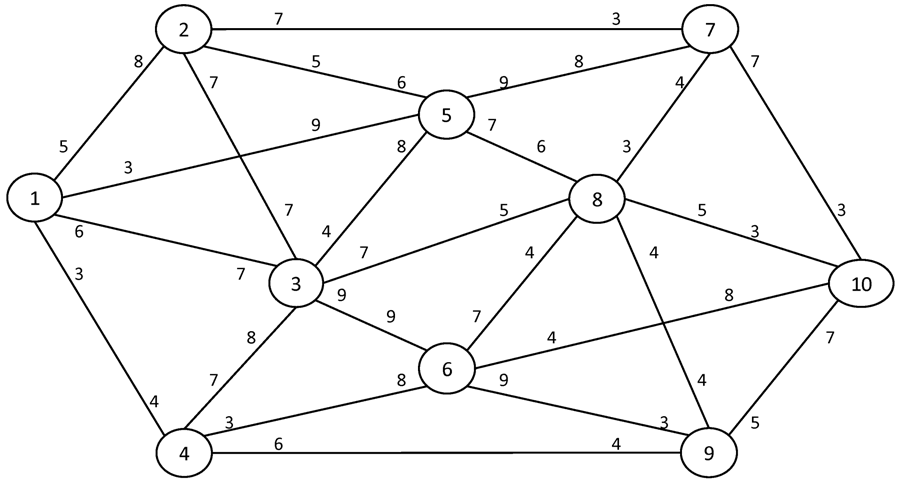
Вариант №6
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8
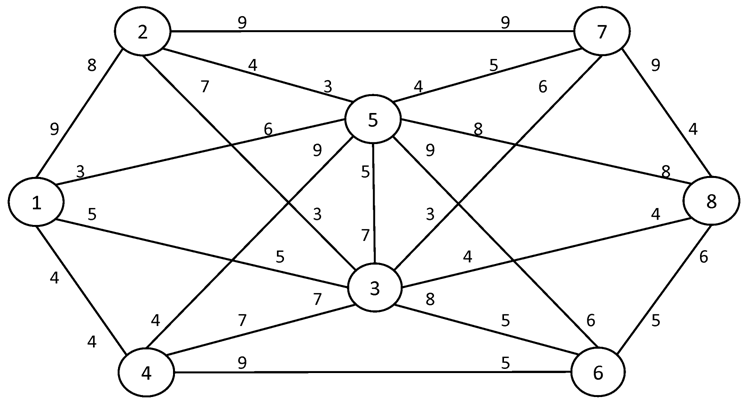
№2. I = 1 S = 10
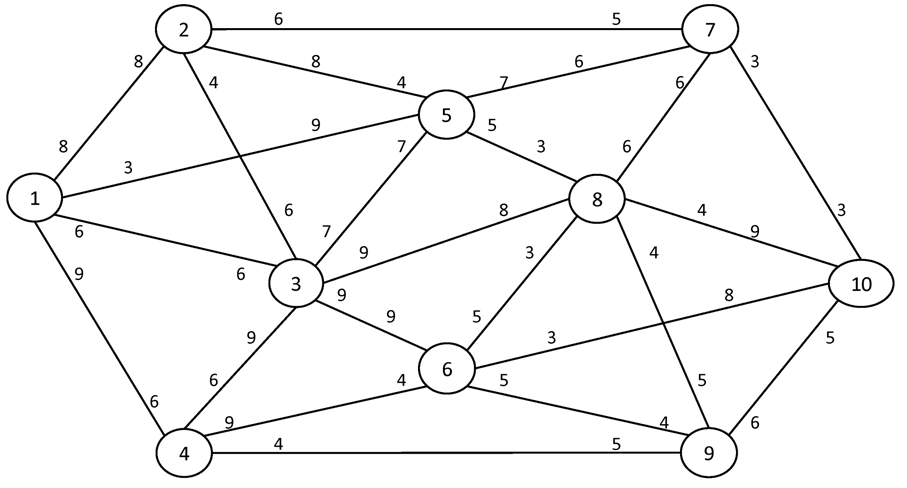
Вариант №7
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8
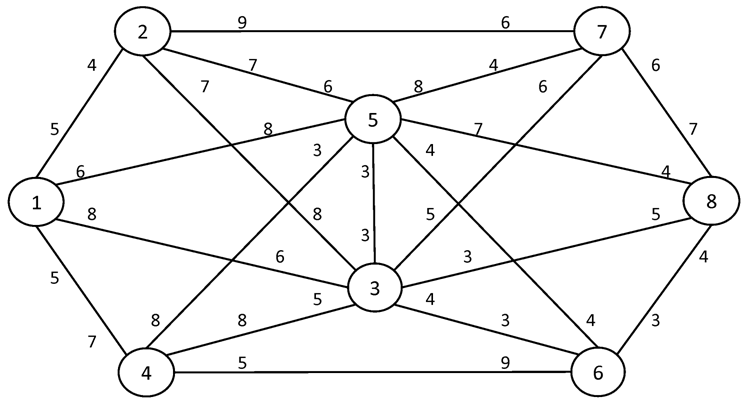
№2. I = 1 S = 10

Вариант №8
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8
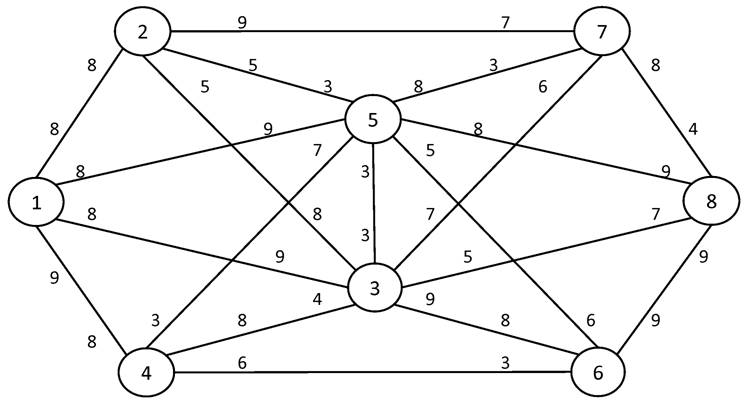
№2. I = 1 S = 10
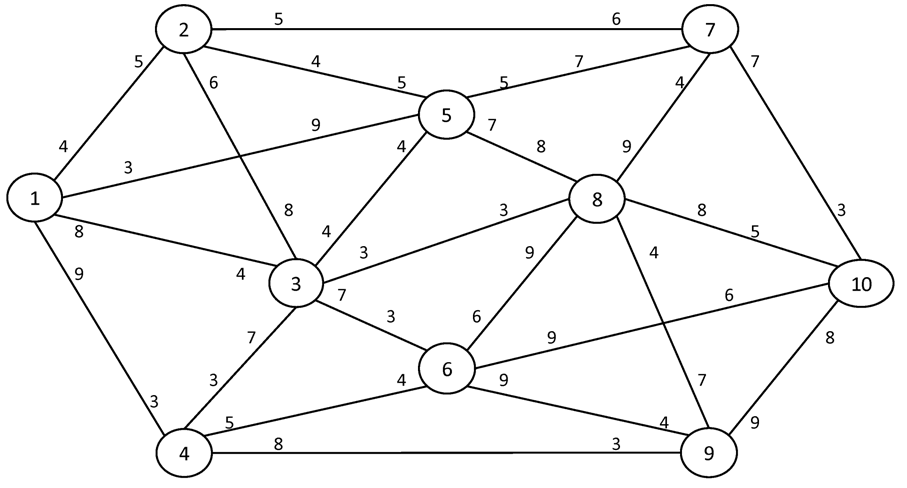
Вариант №9
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8
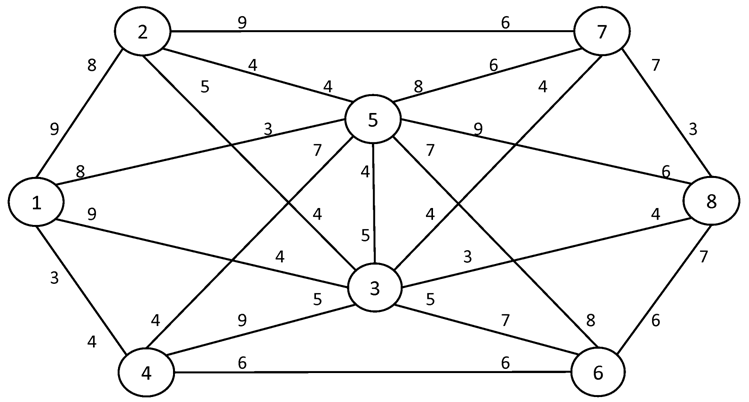
№2. I = 1 S = 10

Вариант №10
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8
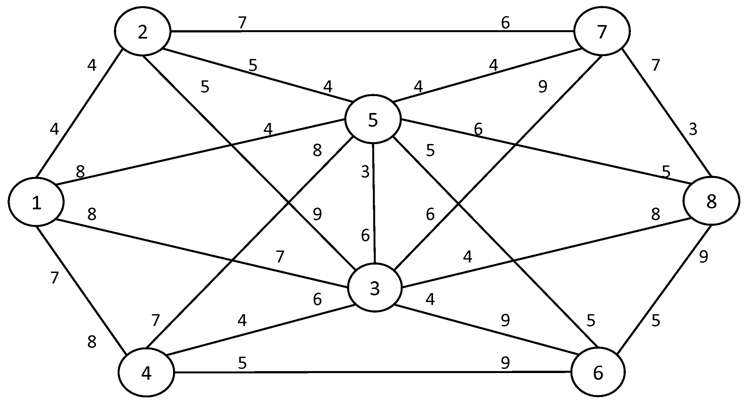
№2. I = 1 S = 10
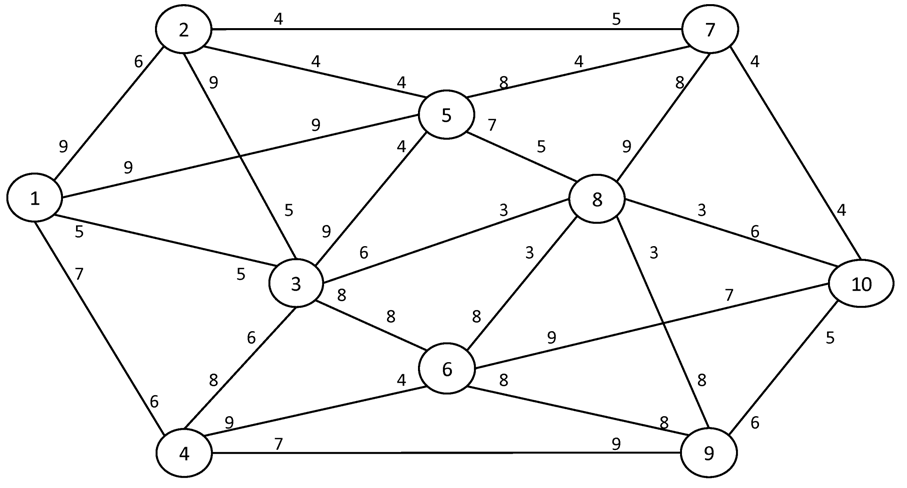
Вариант №11
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8
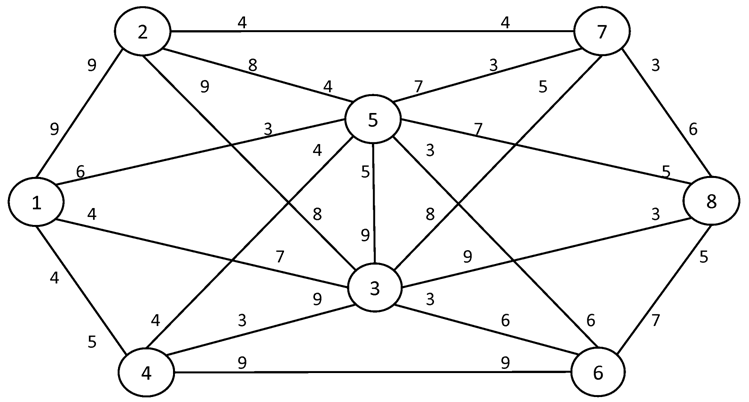
№2. I = 1 S = 10
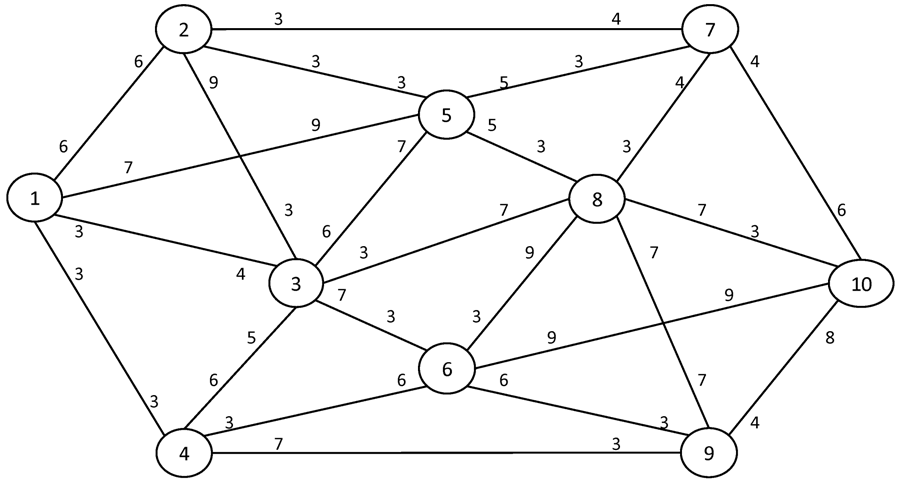
Вариант №12
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8
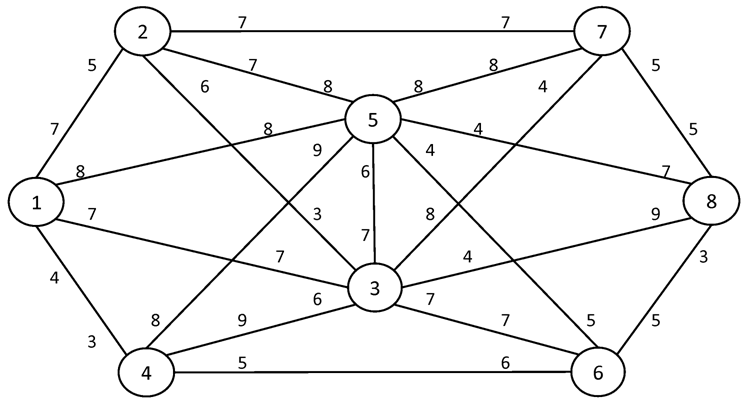
№2. I = 1 S = 10

Вариант №13
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8
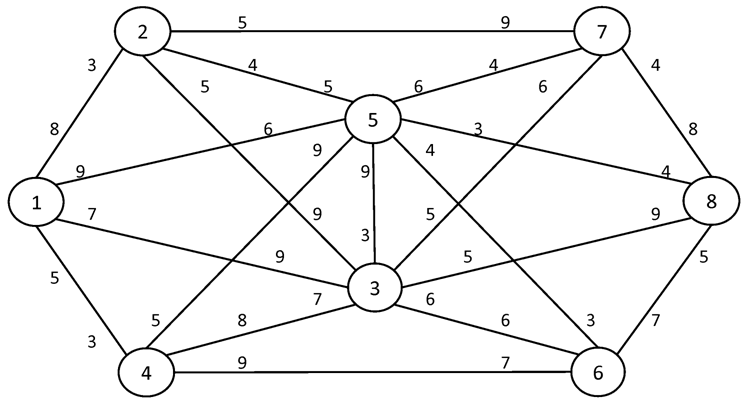
№2. I = 1 S = 10
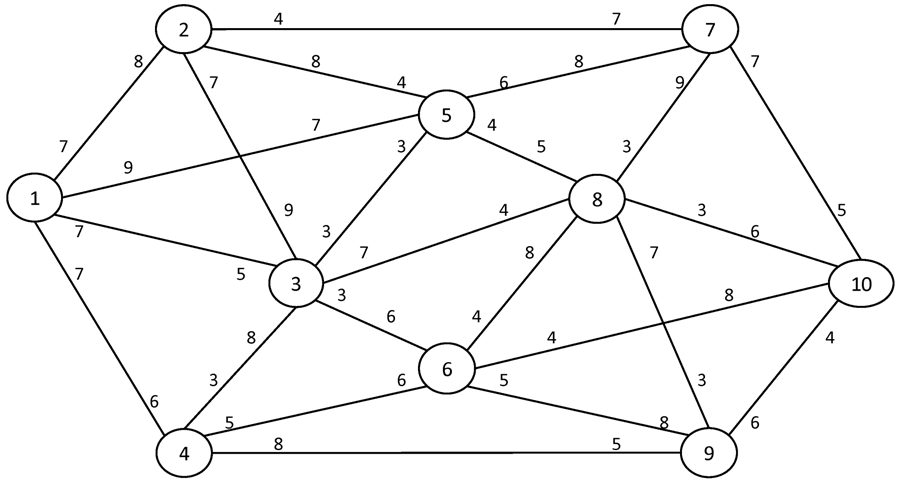
Вариант №14
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8
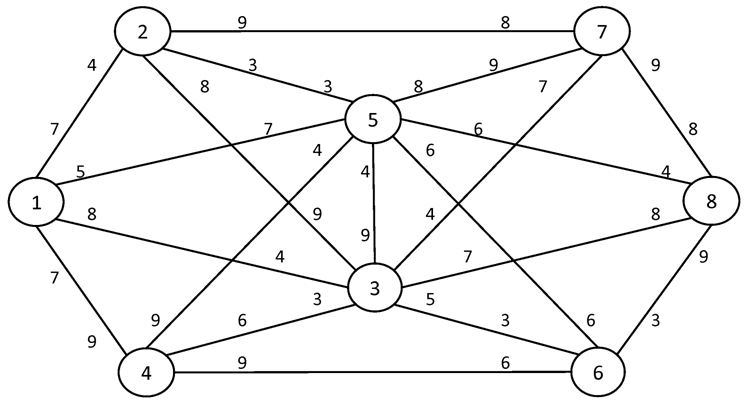
№2. I = 1 S = 10

Вариант №15
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8
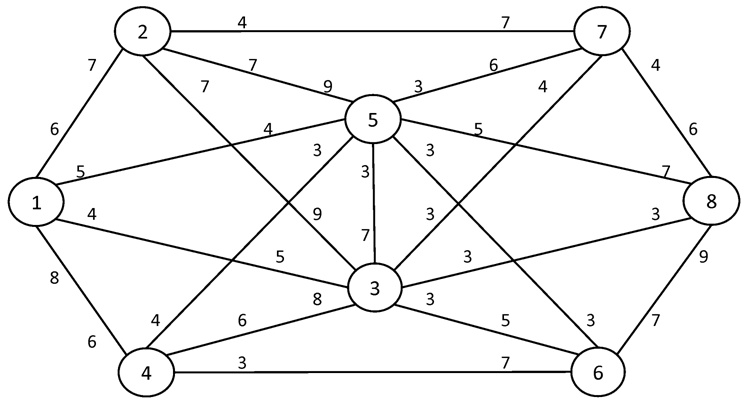
№2. I = 1 S = 10
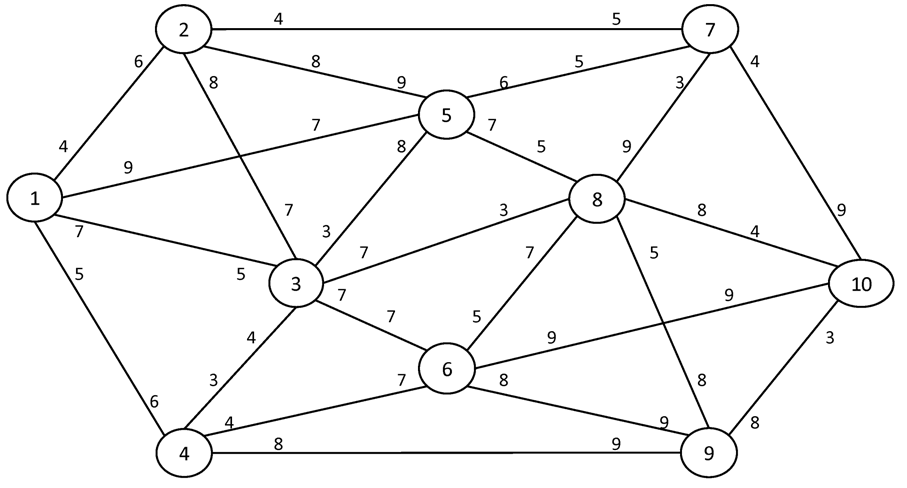
Вариант №16
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8
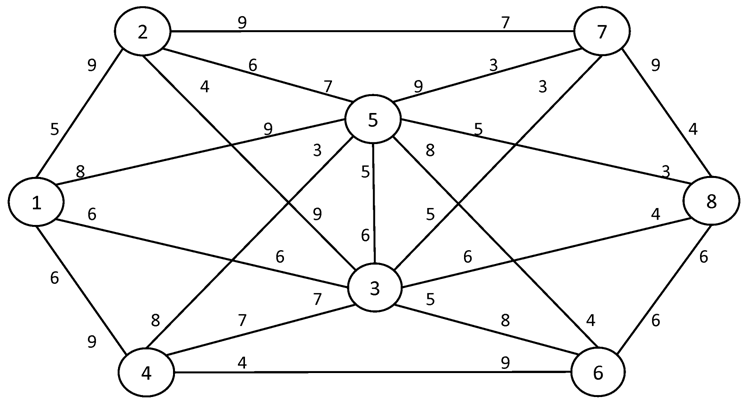
№2. I = 1 S = 10
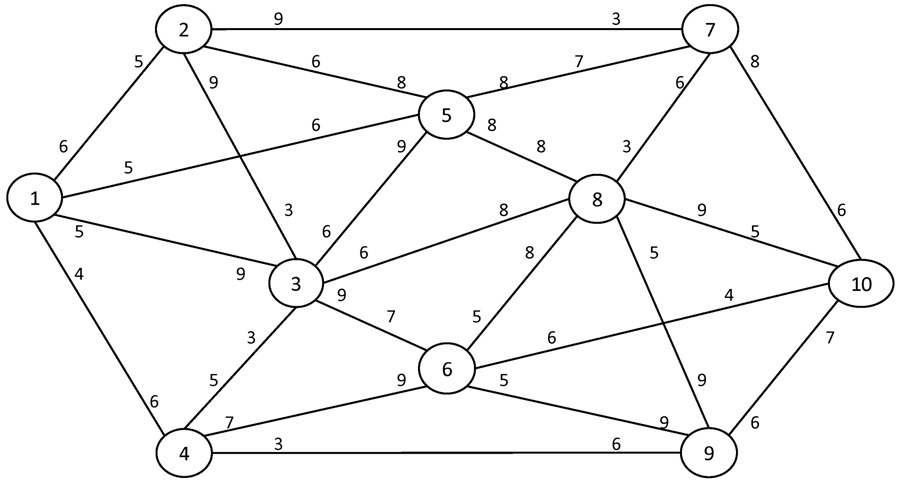
Вариант №17
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8
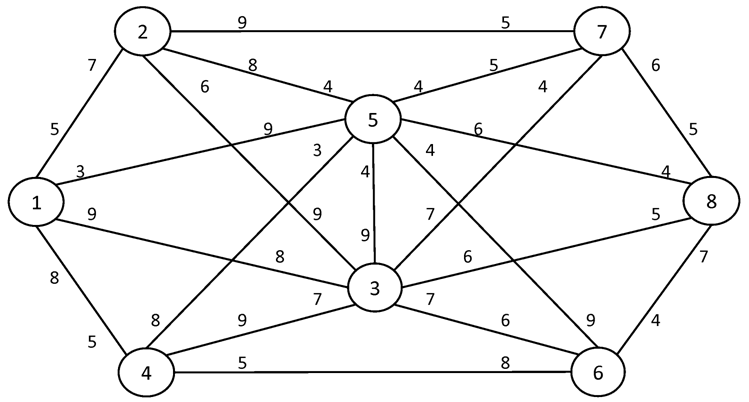
№2. I = 1 S = 10
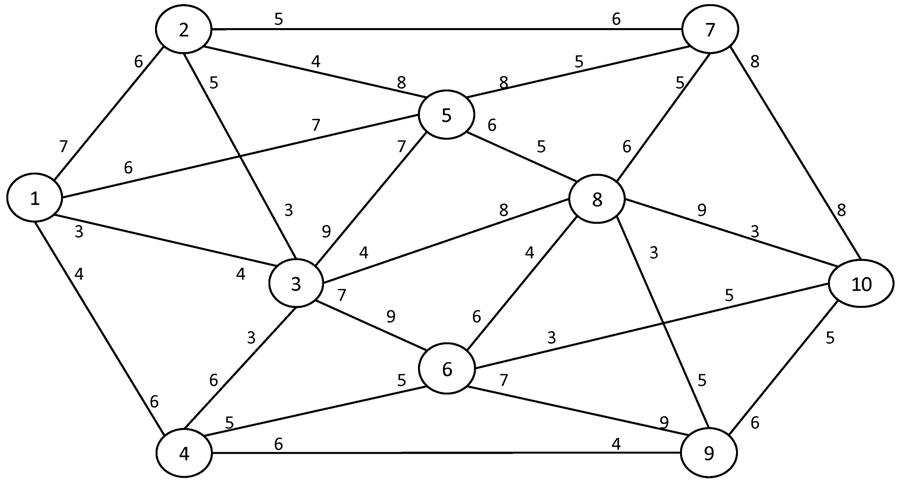
Вариант №18
Найти максимальный поток в сети между истоком I и стоком S.
№1. I = 1 S = 8
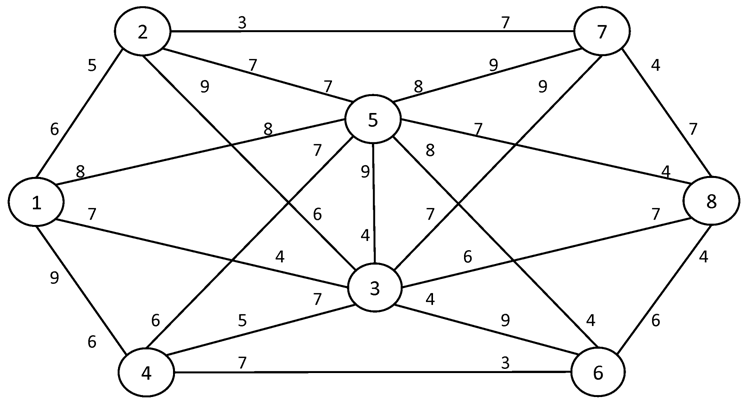
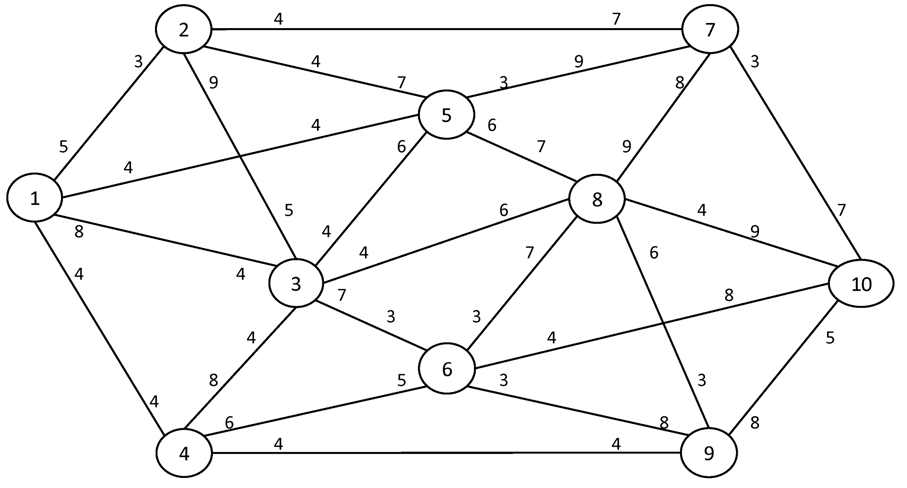
№2. I = 1 S = 10
ВОПРОСЫ ВЫХОДНОГО КОНТРОЛЯ:
- Дайте определение графа, приведите примеры.
- Объясните понятие сети.
- Сформулируйте определение разреза.
- Сформулируйте определение потока.
- Сформулируйте определение максимального потока.
- Объясните суть алгоритма Форда-Фалкерсона.
ДОМАШНЕЕ ЗАДАНИЕ:
Выучить алгоритм Форда-Фалкерсона.