ЭЛЕКТРОННЫЙ ЛАБОРАТОРНЫЙ ПРАКТИКУМ
ПО УЧЕБНОМУ ПРЕДМЕТУ
"ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ"
№19. Решение матричных игр в чистых стратегиях
Цель: научить решать матричные игры в чистых стратегиях.
Оборудование: практикум, тетрадь для лабораторных и практических работ.
Литература:
- Плотников А. Д. Математическое программирование: экспресс-курс. - Мн.: Новое знание, 2007. С. 147-156.
- Таха, Хемди. Введение в исследование операций - М.: Издательский дом "Вильямс", 2005. С. 446-465.
Время выполнения: 2 часа.
ВОПРОСЫ ВХОДНОГО КОНТРОЛЯ:
- Опишите понятие матричной игры.
- Опишите понятие стратегии матричной игры.
- Опишите понятие платежной матрицы матричной игры.
- Опишите правила выбора стратегии в матричной игре.
- Опишите понятие нижней и верхней цены матричной игры.
- Опишите понятие седловой точки матричной игры.
- Опишите процесс поиска решения матричной игры в чистых стратегиях.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:
Матричной игрой в математической теории игр называется игра двух лиц с нулевой суммой, в которой в распоряжении каждого из них имеется конечное множество стратегий. Правила матричной игры определяет платёжная матрица, элементы которой - выигрыши первого игрока, которые являются также проигрышами второго игрока.
Матричная игра является антагонистической игрой. Первый игрок получает максимальный гарантированный (не зависящий от поведения второго игрока) выигрыш, равный цене игры, аналогично, второй игрок добивается минимального гарантированного проигрыша.
Под стратегией понимается совокупность правил (принципов), определяющих выбор варианта действий при каждом личном ходе игрока в зависимости от сложившейся ситуации.
Рассмотрим игру, в которой имеются два участника: первый игрок и второй игрок. Пусть в распоряжении первого игрока имеется m чистых стратегий, а в распоряжении второго игрока - n чистых стратегий.
В платёжной матрице элементами являются числа, выражающие выигрыши и проигрыши игроков. Выигрыши и проигрыши могут выражаться в пунктах, количестве денег или в других единицах.
Составим платёжную матрицу:

Сначала определим величину выигрыша первого игрока, если он использует i-ю чистую стратегию. Если первый игрок использует i-ю чистую стратегию, то логично предположить, что второй игрок будет использовать такую чистую стратегию, благодаря которой выигрыш первого игрока был бы минимальным. В свою очередь первый игрок будет использовать такую чистую стратегию, которая бы обеспечила ему максимальный выигрыш. Исходя из этих условий выигрыш первого игрока, который обозначим как v1, называется максиминным выигрышем или нижней ценой игры.
При решении задач на цену игры и определение стратегии для этих величин у первого игрока следует поступать следующим образом. Из каждой строки выписать значение минимального элемента и уже из них выбрать максимальный. Таким образом, выигрыш первого игрока будет максимальным из минимальных. Отсюда и название - максиминный выигрыш. Номер строки этого элемента и будет номером чистой стратегии, которую выбирает первый игрок.
Теперь определим величину проигрыша второго игрока, если он использует j-ю стратегию. В этом случае первый игрок использует такую свою чистую стратегию, при которой проигрыш второго игрока был бы максимальным. Второй игрок должен выбрать такую чистую стратегию, при которой его проигрыш был бы минимальным. Проигрыш второго игрока, который обозначим как v2, называется минимаксным проигрышем или верхней ценой игры.
Таким образом, первый игрок должен выбрать чистую стратегию, которая обеспечивала бы ему максимальный из минимальных выигрышей. Этот выигрыш (максимин) обозначается так:

Второй игрок должен выбрать свою чистую стратегию так, чтобы его проигрыш был минимальным. Этот проигрыш (минимакс) обозначается так:

Если верхняя и нижняя цена игры одинаковая, то считается, что матричная игра имеет седловую точку. Верно и обратное утверждение: если матричная игра имеет седловую точку, то верхняя и нижняя цены матричной игры одинаковы. Соответствующий элемент одновременно является наименьшим в строке и наибольшим в столбце и равен цене игры.
В этом случае матричная игра имеет решение в чистых стратегиях.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ:
Пример. Дана матричная игра с платёжной матрицей

Найти нижнюю и верхнюю цену игры. Имеет ли данная матричная игра седловую точку? Существует ли решение в чистых стратегиях для данной матричной игры?
Решение.
Справа от платёжной матрицы выпишем наименьшие элементы в её строках и отметим максимальный из них, а снизу от матрицы - наибольшие элементы в столбцах и выберем минимальный из них:
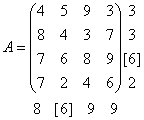
Нижняя цена игры совпадает с верхней ценой игры. Таким образом, цена игры равна 6.
То есть ![]() . Цена игры равна
значению седловой точки
. Цена игры равна
значению седловой точки ![]() .
Максиминная стратегия первого игрока - третья чистая стратегия, а минимаксная стратегия второго
игрока -
вторая чистая стратегия. Данная матричная игра имеет решение в чистых стратегиях.
.
Максиминная стратегия первого игрока - третья чистая стратегия, а минимаксная стратегия второго
игрока -
вторая чистая стратегия. Данная матричная игра имеет решение в чистых стратегиях.
СОДЕРЖАНИЕ РАБОТЫ:
Вариант №1
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
4 |
0 |
4 |
|
A2 |
-5 |
1 |
-1 |
|
A3 |
-5 |
2 |
4 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-5 |
0 |
2 |
-3 |
|
A2 |
-5 |
-1 |
-4 |
4 |
|
A3 |
-2 |
2 |
1 |
-1 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
0 |
-3 |
1 |
2 |
3 |
-1 |
1 |
|
A2 |
3 |
-2 |
1 |
-5 |
0 |
-5 |
-5 |
|
A3 |
-5 |
-4 |
2 |
-1 |
1 |
1 |
-4 |
|
A4 |
-5 |
-4 |
-3 |
1 |
1 |
4 |
-3 |
|
A5 |
-4 |
1 |
-5 |
3 |
-3 |
-3 |
-2 |
|
A6 |
-3 |
-3 |
-3 |
2 |
-5 |
-2 |
4 |
|
A7 |
0 |
-2 |
0 |
-3 |
-4 |
-5 |
-2 |
|
A8 |
-5 |
-4 |
4 |
-4 |
4 |
-2 |
-1 |
Вариант №2
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-5 |
-1 |
-4 |
|
A2 |
-4 |
-1 |
-1 |
|
A3 |
2 |
2 |
1 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-4 |
-2 |
2 |
1 |
|
A2 |
2 |
4 |
0 |
1 |
|
A3 |
1 |
-2 |
-3 |
0 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
3 |
2 |
-1 |
-1 |
4 |
3 |
-5 |
|
A2 |
-1 |
-4 |
2 |
-2 |
4 |
3 |
-3 |
|
A3 |
3 |
-4 |
1 |
0 |
4 |
-4 |
2 |
|
A4 |
2 |
-2 |
4 |
-2 |
-2 |
0 |
-4 |
|
A5 |
1 |
-3 |
-1 |
1 |
-5 |
4 |
-3 |
|
A6 |
1 |
2 |
1 |
0 |
0 |
1 |
-3 |
|
A7 |
-1 |
-2 |
4 |
3 |
3 |
0 |
-5 |
|
A8 |
-2 |
-5 |
-4 |
-2 |
-5 |
2 |
-5 |
Вариант №3
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-2 |
0 |
-5 |
|
A2 |
1 |
-2 |
4 |
|
A3 |
3 |
3 |
-3 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
2 |
3 |
3 |
-5 |
|
A2 |
-4 |
-1 |
4 |
4 |
|
A3 |
-2 |
-1 |
0 |
-3 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
-5 |
4 |
0 |
-1 |
-5 |
-5 |
-3 |
|
A2 |
-3 |
-2 |
-3 |
4 |
-4 |
-4 |
-2 |
|
A3 |
-4 |
0 |
4 |
-3 |
2 |
-1 |
1 |
|
A4 |
-5 |
-3 |
4 |
4 |
0 |
3 |
4 |
|
A5 |
-5 |
-4 |
4 |
1 |
-3 |
3 |
-2 |
|
A6 |
1 |
0 |
-4 |
-2 |
3 |
0 |
1 |
|
A7 |
4 |
-1 |
3 |
1 |
3 |
3 |
-3 |
|
A8 |
-2 |
4 |
-4 |
2 |
-5 |
1 |
4 |
Вариант №4
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
1 |
1 |
-1 |
|
A2 |
-1 |
-3 |
-3 |
|
A3 |
-4 |
-4 |
-3 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-2 |
4 |
-2 |
4 |
|
A2 |
0 |
-5 |
3 |
4 |
|
A3 |
3 |
3 |
-5 |
-4 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
2 |
-5 |
-2 |
1 |
4 |
2 |
1 |
|
A2 |
-3 |
3 |
3 |
-4 |
-3 |
-1 |
-5 |
|
A3 |
3 |
1 |
3 |
1 |
-3 |
-1 |
3 |
|
A4 |
-3 |
-1 |
2 |
0 |
3 |
1 |
-3 |
|
A5 |
-4 |
-3 |
3 |
-3 |
0 |
2 |
3 |
|
A6 |
0 |
-4 |
3 |
-3 |
0 |
0 |
4 |
|
A7 |
-2 |
0 |
2 |
-4 |
0 |
0 |
-4 |
|
A8 |
-4 |
-4 |
-3 |
0 |
1 |
-3 |
0 |
Вариант №5
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
0 |
0 |
-4 |
|
A2 |
-4 |
-5 |
-2 |
|
A3 |
-5 |
1 |
4 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
4 |
1 |
1 |
-4 |
|
A2 |
-2 |
0 |
4 |
-1 |
|
A3 |
2 |
3 |
4 |
3 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
4 |
4 |
-1 |
-2 |
-4 |
-4 |
-5 |
|
A2 |
-4 |
1 |
1 |
4 |
-1 |
-3 |
4 |
|
A3 |
1 |
1 |
-4 |
-1 |
-4 |
3 |
2 |
|
A4 |
0 |
3 |
-1 |
3 |
-2 |
3 |
1 |
|
A5 |
-4 |
2 |
3 |
2 |
-2 |
1 |
0 |
|
A6 |
1 |
2 |
2 |
4 |
-3 |
-5 |
-1 |
|
A7 |
-3 |
-2 |
1 |
-4 |
3 |
-2 |
4 |
|
A8 |
-3 |
-2 |
-3 |
2 |
-4 |
-5 |
-1 |
Вариант №6
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-4 |
4 |
-1 |
|
A2 |
2 |
-3 |
-2 |
|
A3 |
-5 |
3 |
2 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-3 |
-4 |
0 |
-2 |
|
A2 |
4 |
4 |
-2 |
0 |
|
A3 |
3 |
2 |
-2 |
-3 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
-1 |
3 |
1 |
-1 |
-1 |
2 |
3 |
|
A2 |
-1 |
0 |
4 |
-3 |
1 |
-4 |
-1 |
|
A3 |
2 |
-2 |
-4 |
-5 |
2 |
-1 |
-1 |
|
A4 |
0 |
-1 |
-5 |
-2 |
4 |
4 |
-2 |
|
A5 |
4 |
2 |
4 |
-2 |
2 |
-4 |
1 |
|
A6 |
-4 |
2 |
-3 |
2 |
1 |
-4 |
-1 |
|
A7 |
-3 |
-3 |
4 |
4 |
-3 |
0 |
-4 |
|
A8 |
-5 |
-2 |
3 |
-5 |
3 |
3 |
4 |
Вариант №7
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-2 |
1 |
-4 |
|
A2 |
0 |
3 |
0 |
|
A3 |
-1 |
3 |
-5 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
3 |
3 |
-5 |
3 |
|
A2 |
1 |
0 |
4 |
-3 |
|
A3 |
-5 |
-2 |
-5 |
-3 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
-4 |
-4 |
-2 |
2 |
-1 |
-4 |
4 |
|
A2 |
-1 |
-5 |
-3 |
4 |
-2 |
2 |
2 |
|
A3 |
-4 |
-5 |
-3 |
2 |
1 |
4 |
-1 |
|
A4 |
-3 |
-5 |
-5 |
-4 |
1 |
0 |
-1 |
|
A5 |
-2 |
0 |
4 |
0 |
3 |
1 |
-4 |
|
A6 |
0 |
3 |
2 |
-1 |
-2 |
-1 |
-2 |
|
A7 |
4 |
0 |
4 |
2 |
-4 |
4 |
-1 |
|
A8 |
3 |
-5 |
-2 |
1 |
-5 |
3 |
4 |
Вариант №8
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-4 |
-2 |
0 |
|
A2 |
2 |
0 |
0 |
|
A3 |
-5 |
0 |
-2 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-1 |
-1 |
-5 |
0 |
|
A2 |
0 |
-3 |
-1 |
-2 |
|
A3 |
-3 |
-1 |
-5 |
-3 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
-1 |
-5 |
-1 |
0 |
1 |
-5 |
0 |
|
A2 |
0 |
1 |
3 |
2 |
2 |
-4 |
-1 |
|
A3 |
0 |
-4 |
1 |
2 |
4 |
-2 |
-1 |
|
A4 |
-3 |
0 |
-3 |
-5 |
-2 |
3 |
0 |
|
A5 |
0 |
4 |
-2 |
1 |
3 |
2 |
1 |
|
A6 |
-3 |
-4 |
-4 |
4 |
0 |
0 |
4 |
|
A7 |
1 |
0 |
1 |
-3 |
-2 |
-4 |
2 |
|
A8 |
-3 |
1 |
-1 |
-1 |
1 |
2 |
-4 |
Вариант №9
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
0 |
-4 |
0 |
|
A2 |
-2 |
-4 |
4 |
|
A3 |
-5 |
2 |
0 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-4 |
4 |
-1 |
2 |
|
A2 |
-3 |
-5 |
0 |
3 |
|
A3 |
-1 |
3 |
-1 |
0 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
-5 |
0 |
2 |
4 |
1 |
3 |
-3 |
|
A2 |
-3 |
3 |
-4 |
-4 |
4 |
0 |
1 |
|
A3 |
4 |
1 |
1 |
-2 |
0 |
4 |
4 |
|
A4 |
4 |
0 |
-2 |
4 |
-1 |
-1 |
-3 |
|
A5 |
-4 |
1 |
-5 |
3 |
-2 |
1 |
0 |
|
A6 |
0 |
2 |
-2 |
0 |
-5 |
2 |
-1 |
|
A7 |
2 |
-5 |
2 |
0 |
-4 |
1 |
-5 |
|
A8 |
4 |
-4 |
-4 |
-3 |
0 |
0 |
-5 |
Вариант №10
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-5 |
-2 |
4 |
|
A2 |
-4 |
-2 |
-5 |
|
A3 |
-4 |
-4 |
-5 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-2 |
1 |
4 |
-4 |
|
A2 |
-2 |
3 |
-3 |
3 |
|
A3 |
-1 |
-4 |
0 |
-3 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
-1 |
0 |
-1 |
-2 |
3 |
-4 |
-4 |
|
A2 |
-1 |
4 |
0 |
2 |
-5 |
-1 |
-1 |
|
A3 |
-2 |
-1 |
-2 |
2 |
2 |
-3 |
0 |
|
A4 |
4 |
-1 |
3 |
-3 |
-1 |
2 |
-4 |
|
A5 |
4 |
-2 |
2 |
-2 |
4 |
3 |
0 |
|
A6 |
3 |
0 |
3 |
-1 |
3 |
4 |
2 |
|
A7 |
-4 |
2 |
3 |
3 |
2 |
3 |
-1 |
|
A8 |
3 |
-1 |
2 |
-1 |
-3 |
1 |
0 |
Вариант №11
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-4 |
0 |
-5 |
|
A2 |
-1 |
-1 |
-5 |
|
A3 |
0 |
1 |
2 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-1 |
-5 |
0 |
4 |
|
A2 |
0 |
4 |
-1 |
-3 |
|
A3 |
3 |
-2 |
3 |
2 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
1 |
4 |
-2 |
2 |
3 |
1 |
-4 |
|
A2 |
3 |
-5 |
3 |
2 |
-4 |
-5 |
1 |
|
A3 |
4 |
3 |
-5 |
-1 |
3 |
-3 |
0 |
|
A4 |
-5 |
-1 |
3 |
-4 |
4 |
3 |
4 |
|
A5 |
-5 |
-1 |
1 |
4 |
3 |
3 |
0 |
|
A6 |
0 |
1 |
1 |
1 |
-2 |
-2 |
2 |
|
A7 |
2 |
0 |
-2 |
-1 |
4 |
4 |
4 |
|
A8 |
1 |
-4 |
-1 |
-1 |
0 |
-4 |
0 |
Вариант №12
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
0 |
0 |
0 |
|
A2 |
3 |
3 |
-3 |
|
A3 |
2 |
0 |
-3 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
2 |
-2 |
-4 |
-4 |
|
A2 |
-2 |
-4 |
-2 |
3 |
|
A3 |
0 |
3 |
2 |
-2 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
4 |
-1 |
2 |
-5 |
4 |
4 |
-1 |
|
A2 |
-3 |
-4 |
-1 |
-3 |
1 |
4 |
-5 |
|
A3 |
-5 |
-5 |
2 |
0 |
-4 |
-5 |
-4 |
|
A4 |
-3 |
0 |
-5 |
2 |
3 |
1 |
-1 |
|
A5 |
3 |
1 |
4 |
2 |
-2 |
-3 |
0 |
|
A6 |
-5 |
3 |
3 |
4 |
-3 |
-2 |
-3 |
|
A7 |
-5 |
-2 |
-5 |
-1 |
-4 |
-3 |
-4 |
|
A8 |
-3 |
-5 |
4 |
1 |
2 |
-4 |
1 |
Вариант №13
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
4 |
1 |
-2 |
|
A2 |
-5 |
-3 |
4 |
|
A3 |
-1 |
0 |
0 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
0 |
-3 |
1 |
-1 |
|
A2 |
4 |
-3 |
4 |
1 |
|
A3 |
3 |
1 |
3 |
-4 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
-3 |
-5 |
-3 |
1 |
-2 |
-2 |
0 |
|
A2 |
0 |
4 |
-5 |
0 |
-5 |
4 |
-4 |
|
A3 |
-3 |
0 |
3 |
4 |
-1 |
3 |
-1 |
|
A4 |
2 |
0 |
-3 |
-1 |
3 |
-4 |
-5 |
|
A5 |
-4 |
-2 |
3 |
-4 |
-3 |
-1 |
2 |
|
A6 |
0 |
-5 |
-1 |
4 |
1 |
4 |
-5 |
|
A7 |
0 |
-1 |
1 |
1 |
0 |
3 |
-5 |
|
A8 |
-1 |
2 |
3 |
-3 |
-5 |
1 |
-1 |
Вариант №14
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
0 |
-5 |
-4 |
|
A2 |
0 |
-4 |
0 |
|
A3 |
-1 |
1 |
-3 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-1 |
2 |
-1 |
-2 |
|
A2 |
1 |
-1 |
-2 |
-5 |
|
A3 |
2 |
3 |
-1 |
-3 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
-5 |
0 |
3 |
-3 |
-3 |
-5 |
1 |
|
A2 |
0 |
4 |
4 |
-3 |
3 |
-3 |
-5 |
|
A3 |
-5 |
-3 |
-2 |
-1 |
-1 |
0 |
4 |
|
A4 |
-4 |
-3 |
3 |
-4 |
-1 |
-2 |
-5 |
|
A5 |
-2 |
3 |
-1 |
-4 |
-3 |
-3 |
-1 |
|
A6 |
0 |
-3 |
-3 |
3 |
-1 |
3 |
-5 |
|
A7 |
-2 |
-1 |
0 |
1 |
-5 |
1 |
-1 |
|
A8 |
-5 |
1 |
-3 |
-1 |
4 |
-3 |
3 |
Вариант №15
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-3 |
-5 |
-5 |
|
A2 |
3 |
1 |
1 |
|
A3 |
-3 |
-5 |
-1 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-5 |
0 |
-5 |
0 |
|
A2 |
0 |
-5 |
-4 |
1 |
|
A3 |
4 |
2 |
4 |
3 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
2 |
-3 |
0 |
-2 |
2 |
1 |
-3 |
|
A2 |
-4 |
-3 |
2 |
-3 |
4 |
1 |
-3 |
|
A3 |
-4 |
-4 |
-5 |
3 |
-4 |
3 |
-3 |
|
A4 |
-5 |
0 |
-5 |
-5 |
-5 |
3 |
-5 |
|
A5 |
0 |
1 |
0 |
-4 |
-2 |
-5 |
-1 |
|
A6 |
3 |
0 |
-1 |
3 |
-5 |
4 |
4 |
|
A7 |
-3 |
-2 |
-2 |
-4 |
3 |
-3 |
3 |
|
A8 |
4 |
0 |
-5 |
0 |
-4 |
0 |
2 |
Вариант №16
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
1 |
0 |
-2 |
|
A2 |
2 |
2 |
-3 |
|
A3 |
1 |
0 |
-4 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-4 |
0 |
1 |
2 |
|
A2 |
-2 |
1 |
0 |
4 |
|
A3 |
-4 |
3 |
-2 |
2 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
-3 |
1 |
4 |
-4 |
1 |
-3 |
1 |
|
A2 |
-5 |
-1 |
1 |
-3 |
-1 |
2 |
-3 |
|
A3 |
-5 |
-4 |
-4 |
-2 |
2 |
-3 |
2 |
|
A4 |
-4 |
-3 |
0 |
-3 |
-1 |
0 |
-3 |
|
A5 |
-5 |
-5 |
-1 |
-3 |
-3 |
-5 |
-2 |
|
A6 |
3 |
-1 |
0 |
-5 |
4 |
-5 |
0 |
|
A7 |
1 |
0 |
-2 |
-3 |
-5 |
-5 |
1 |
|
A8 |
-1 |
3 |
3 |
-4 |
-5 |
4 |
-4 |
Вариант №17
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-1 |
-2 |
4 |
|
A2 |
-4 |
1 |
-2 |
|
A3 |
4 |
-2 |
-4 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-5 |
-4 |
1 |
3 |
|
A2 |
-4 |
2 |
1 |
-3 |
|
A3 |
2 |
-3 |
-4 |
0 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
1 |
-4 |
-5 |
-1 |
-1 |
1 |
1 |
|
A2 |
-3 |
1 |
-4 |
-4 |
-5 |
-3 |
-2 |
|
A3 |
-5 |
0 |
3 |
-3 |
1 |
0 |
-3 |
|
A4 |
-2 |
-2 |
-5 |
-2 |
-3 |
-1 |
2 |
|
A5 |
-4 |
0 |
-2 |
2 |
3 |
0 |
3 |
|
A6 |
-3 |
4 |
2 |
-3 |
2 |
-2 |
-4 |
|
A7 |
0 |
3 |
4 |
1 |
1 |
3 |
1 |
|
A8 |
-5 |
-2 |
-1 |
1 |
1 |
-3 |
-2 |
Вариант №18
Для указанной матричной игры найдите ее верхнюю и нижнюю цену, определите ее решение в чистых стратегиях, если оно существует.
№1.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
3 |
4 |
-5 |
|
A2 |
-3 |
-4 |
4 |
|
A3 |
-4 |
-5 |
3 |
№2.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-1 |
-3 |
1 |
0 |
|
A2 |
3 |
1 |
-5 |
-5 |
|
A3 |
4 |
-4 |
-4 |
3 |
№3.
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | |
|---|---|---|---|---|---|---|---|
|
A1 |
-1 |
-5 |
2 |
0 |
1 |
-5 |
-5 |
|
A2 |
-4 |
3 |
-4 |
-4 |
-3 |
-1 |
-2 |
|
A3 |
4 |
2 |
-5 |
0 |
-1 |
4 |
-1 |
|
A4 |
-5 |
0 |
-2 |
4 |
-3 |
3 |
-1 |
|
A5 |
-3 |
-1 |
1 |
-1 |
-4 |
0 |
-2 |
|
A6 |
4 |
-3 |
1 |
-1 |
3 |
-5 |
4 |
|
A7 |
4 |
-3 |
-4 |
-2 |
-5 |
-1 |
2 |
|
A8 |
-2 |
4 |
-2 |
2 |
-4 |
-2 |
-1 |
ВОПРОСЫ ВЫХОДНОГО КОНТРОЛЯ:
- Опишите понятие матричной игры.
- Опишите понятие стратегии матричной игры.
- Опишите понятие платежной матрицы матричной игры.
- Опишите правила выбора стратегии в матричной игре.
- Опишите понятие нижней и верхней цены матричной игры.
- Опишите понятие седловой точки матричной игры.
- Опишите процесс поиска решения матричной игры в чистых стратегиях.
ДОМАШНЕЕ ЗАДАНИЕ:
Выучить процесс поиска решения матричной игры в чистых стратегиях.