ЭЛЕКТРОННЫЙ ЛАБОРАТОРНЫЙ ПРАКТИКУМ
ПО УЧЕБНОМУ ПРЕДМЕТУ
"ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ"
№20. Решение матричных игр в смешанных стратегиях
Цель: научить решать матричные игры в смешанных стратегиях.
Оборудование: практикум, тетрадь для лабораторных и практических работ.
Литература:
- Плотников А. Д. Математическое программирование: экспресс-курс. - Мн.: Новое знание, 2007. С. 147-156.
- Таха, Хемди. Введение в исследование операций - М.: Издательский дом "Вильямс", 2005. С. 446-465.
Время выполнения: 2 часа.
ВОПРОСЫ ВХОДНОГО КОНТРОЛЯ:
- Опишите понятие матричной игры.
- Опишите понятие стратегии матричной игры.
- Опишите понятие платежной матрицы матричной игры.
- Опишите правила выбора стратегии в матричной игре.
- Опишите понятие нижней и верхней цены матричной игры.
- Опишите понятие седловой точки матричной игры.
- Дайте понятие смешанной стратегии игрока в матричной игре.
- Приведите алгоритм решения матричной игры в смешанных стратегиях
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:
В большинстве случаев матричная игра не имеет седловой точки, поэтому соответствующая матричная игра не имеет решений в чистых стратегиях.
Но она имеет решение в оптимальных смешанных стратегиях. Для их нахождения нужно принять, что игра повторяется достаточное число раз, чтобы на основании опыта можно было предположить, какая стратегия является более предпочтительной. Поэтому решение связывается с понятием вероятности и среднего (математического ожидания). В окончательном же решении есть и аналог седловой точки (то есть равенства нижней и верхней цены игры), и аналог соответствующих им стратегий.
Итак, чтобы чтобы первый игрок получил максимальный средний выигрыш и чтобы средний проигрыш второго игрока был минимальным, чистые стратегии следует использовать с определённой вероятностью.
Если первый игрок использует чистые стратегии с вероятностями 
, то
вектор 
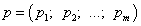называется смешанной стратегией первого игрока. Иначе говоря,
это "смесь" чистых стратегий. При этом сумма этих вероятностей равна единице:
.
Если второй игрок использует чистые стратегии с вероятностями 
, то
вектор 
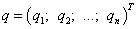называется смешанной стратегией второго игрока. При этом сумма
этих вероятностей равна единице:
.
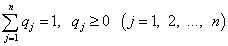Если первый игрок использует смешанную стратегию p, а второй игрок - смешанную стратегию q, то имеет
смысл математическое ожидание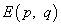 
выигрыша первого игрока (проигрыша
второго игрока). Чтобы его найти, нужно перемножить вектор смешанной стратении первого игрока
(который будет матрицей из одной строки), платёжную матрицу и вектор смешанной стратегии второго
игрока (который будет матрицей из одного столбца):
.
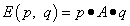Оптимальной смешанной стратегией первого игрока называется такая смешанная стратегия 
, которая обеспечивала бы ему максимальный средний выигрыш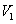 
, если игра повторяется достаточное число раз.
Оптимальной смешанной стратегией второго игрока называется такая смешанная стратегия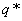 
, которая обеспечивала бы ему минимальный средний проигрыш 
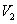, если игра повторяется достаточное число раз.
По аналогии с обозначениями максимина и минимакса в случах чистых стратегий оптимальные смешанные стратегии обозначаются так (и увязываются с математическим ожиданием, то есть средним, выигрыша первого игрока и проигрыша второго игрока):
,
.
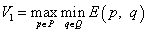В таком случае для функции E существует седловая точка, что означает равенство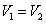 
.
Для того, чтобы найти оптимальные смешанные стратегии и седловую точку, то есть решить матричную игру в смешанных стратегиях, нужно свести матричную игру к задаче линейного программирования, то есть к оптимизационной задаче, и решить соответствующую задачу линейного программирования.
Сведение матричной игры к задаче линейного программирования
Для того, чтобы решить матричную игру в смешанных стратегиях, нужно составить прямую задачу линейного программирования и двойственную ей задачу. В двойственной задаче расширенная матрица, в которой хранятся коэффициенты при переменных в системе ограничений, свободные члены и коэффициенты при переменных в функции цели, транспонируется. При этом минимуму функции цели исходной задачи ставится в соответствие максимум в двойственной задаче.
Функция цели в прямой задаче линейного программирования:
.
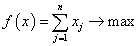Система ограничений в прямой задаче линейного программирования:
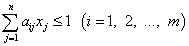
Функция цели в двойственной задаче:
.
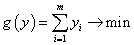Система ограничений в двойственной задаче:
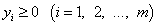
Оптимальный план прямой задачи линейного программирования обозначим
,
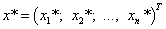а оптимальный план двойственной задачи обозначим
Линейные формы для соответствующих оптимальных планов обозначим 
и 
, а находить их нужно как суммы соответствующих координат оптимальных
планов.
В соответствии определениям предыдущего параграфа и координатами оптимальных планов, в силе следующие смешанные стратегии первого и второго игроков:
,
.
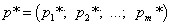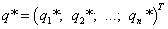Цена игры следующим образом выражается через линейные формы оптимальных планов:
,
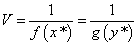то есть является величиной, обратной суммам координат оптимальных планов.
Формулы для нахождения оптимальных смешанных стратегий соответственно первого и второго игроков:
,
,
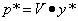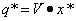в которых вторые сомножители - векторы. Оптимальные смешанные стратегии также являются векторами. Поэтому, умножив число (цену игры) на вектор (с координатами оптимальных планов) получим также вектор.
Игры с матрицей 2 Х 2
Пусть дана игра с платёжной матрицей
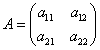
Если эта матричная игра имеет седловую точку, то она имеет решение в чистых стратегиях.
Если же игра не имеет седловой точки, то она имеет решение в оптимальных смешанных стратегиях. Для этого простейшего случая матричной игры при её решениях путём сведения к задаче линейного программирования были найдены формулы стратегий игроков и цены игры, благодаря которым такая игра решается менее трудоёмким способом.
Формула для нахождения оптимальной смешанной стратегии первого игрока:
.
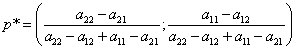Формула для нахождения оптимальной смешанной стратегии второго игрока:
.
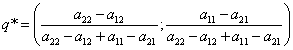Формула для нахождения цены игры:
.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ:
Пример №1. Дана матричная игра с платёжной матрицей
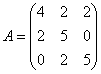
Найти цену игры V и оптимальные смешанные стратеги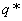и 
и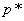 
.
Решение.
Составляем соответствующую данной матричной игре задачу линейного программирования:
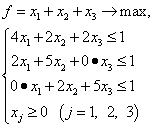
Приводим задачу к канонической форме и решаем задачу и двойственную ей задачу симплекс-методом.
Получаем решение прямой задачи:
.
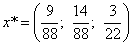Находим линейную форму оптимальных планов как сумму найденных координат:
.
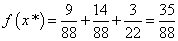Получаем решение двойственной задачи:
.
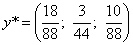Находим линейную форму оптимальных планов как сумму найденных координат:
.
Находим цену игры:
.
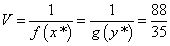Находим оптимальную смешанную стратегию первого игрока:
.
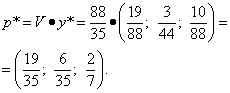Находим оптимальную смешанную стратегию второго игрока:
.
Пример №2.Дана матричная игра с платёжной матрицей
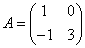
Найти оптимальные смешанные стратегии игроков и цену игры.
Решение.
Оптимальные смешанные стратегии первого игрока получаем по соответствующей из приведённых формул:
.
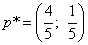Оптимальные смешанные стратегии второго игрока получаем также по соответствующей формуле:
.
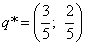Цена игры:
.
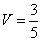СОДЕРЖАНИЕ РАБОТЫ:
Вариант №1
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
2 |
-1 |
|
A2 |
5 |
3 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-4 |
3 |
-3 |
|
A2 |
-5 |
3 |
2 |
|
A3 |
0 |
2 |
2 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-9 |
-6 |
8 |
-2 |
|
A2 |
-1 |
5 |
-3 |
-5 |
|
A3 |
-1 |
-9 |
-4 |
-6 |
|
A4 |
1 |
7 |
-3 |
0 |
Вариант №2
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
1 |
6 |
|
A2 |
-3 |
2 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
3 |
-2 |
2 |
|
A2 |
0 |
-4 |
-3 |
|
A3 |
3 |
-2 |
-2 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-5 |
2 |
5 |
1 |
|
A2 |
6 |
6 |
-8 |
-9 |
|
A3 |
-5 |
6 |
-3 |
-7 |
|
A4 |
-4 |
-9 |
-6 |
-2 |
Вариант №3
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
0 |
2 |
|
A2 |
7 |
5 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-1 |
-2 |
3 |
|
A2 |
-2 |
-3 |
3 |
|
A3 |
1 |
-1 |
-2 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-4 |
-6 |
7 |
-10 |
|
A2 |
7 |
-6 |
-1 |
1 |
|
A3 |
2 |
5 |
-9 |
-5 |
|
A4 |
-2 |
-6 |
-9 |
5 |
Вариант №4
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
0 |
1 |
|
A2 |
-1 |
1 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-4 |
1 |
1 |
|
A2 |
4 |
0 |
4 |
|
A3 |
4 |
2 |
-2 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-3 |
8 |
-7 |
2 |
|
A2 |
4 |
9 |
1 |
0 |
|
A3 |
-8 |
-2 |
7 |
5 |
|
A4 |
6 |
5 |
6 |
7 |
Вариант №5
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
2 |
-5 |
|
A2 |
-4 |
4 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
1 |
3 |
-2 |
|
A2 |
-2 |
-5 |
-3 |
|
A3 |
1 |
1 |
4 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
0 |
9 |
-6 |
4 |
|
A2 |
-6 |
-5 |
6 |
7 |
|
A3 |
3 |
4 |
-6 |
0 |
|
A4 |
-6 |
-5 |
-9 |
-2 |
Вариант №6
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
3 |
-2 |
|
A2 |
6 |
5 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-5 |
4 |
3 |
|
A2 |
3 |
4 |
2 |
|
A3 |
0 |
0 |
3 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
1 |
-1 |
-4 |
8 |
|
A2 |
1 |
2 |
-1 |
2 |
|
A3 |
-9 |
2 |
-1 |
-10 |
|
A4 |
9 |
7 |
-4 |
7 |
Вариант №7
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
-3 |
-1 |
|
A2 |
2 |
-2 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
3 |
-2 |
4 |
|
A2 |
2 |
3 |
3 |
|
A3 |
0 |
-5 |
-2 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
4 |
0 |
4 |
-6 |
|
A2 |
-10 |
-8 |
-6 |
8 |
|
A3 |
2 |
3 |
3 |
1 |
|
A4 |
6 |
1 |
3 |
-2 |
Вариант №8
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
4 |
-4 |
|
A2 |
-4 |
2 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-5 |
2 |
-2 |
|
A2 |
4 |
-3 |
4 |
|
A3 |
-3 |
-1 |
0 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-8 |
4 |
-10 |
-2 |
|
A2 |
-5 |
-3 |
-9 |
5 |
|
A3 |
5 |
8 |
5 |
-9 |
|
A4 |
8 |
2 |
4 |
8 |
Вариант №9
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
3 |
-4 |
|
A2 |
4 |
-1 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-2 |
-5 |
2 |
|
A2 |
-1 |
-1 |
-2 |
|
A3 |
4 |
-4 |
2 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
9 |
-9 |
7 |
5 |
|
A2 |
-4 |
0 |
9 |
2 |
|
A3 |
-7 |
0 |
-6 |
1 |
|
A4 |
2 |
9 |
-7 |
-4 |
Вариант №10
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
1 |
-4 |
|
A2 |
-4 |
3 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-5 |
1 |
3 |
|
A2 |
-1 |
-4 |
-3 |
|
A3 |
-5 |
4 |
0 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
8 |
9 |
-2 |
8 |
|
A2 |
-10 |
6 |
7 |
7 |
|
A3 |
-4 |
1 |
-8 |
5 |
|
A4 |
-4 |
0 |
1 |
0 |
Вариант №11
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
4 |
3 |
|
A2 |
-4 |
2 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-4 |
4 |
-3 |
|
A2 |
2 |
0 |
1 |
|
A3 |
-2 |
-4 |
-1 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
1 |
-9 |
-1 |
9 |
|
A2 |
-10 |
-5 |
0 |
5 |
|
A3 |
2 |
1 |
-7 |
-4 |
|
A4 |
-2 |
-7 |
0 |
-10 |
Вариант №12
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
6 |
5 |
|
A2 |
-4 |
-1 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
4 |
-2 |
1 |
|
A2 |
4 |
-2 |
-1 |
|
A3 |
4 |
2 |
1 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-3 |
-3 |
-1 |
3 |
|
A2 |
-1 |
4 |
0 |
3 |
|
A3 |
5 |
-5 |
-5 |
-10 |
|
A4 |
5 |
-8 |
-9 |
8 |
Вариант №13
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
-2 |
4 |
|
A2 |
5 |
4 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
2 |
1 |
3 |
|
A2 |
-3 |
3 |
-1 |
|
A3 |
-3 |
-1 |
0 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
1 |
2 |
-5 |
6 |
|
A2 |
-8 |
-5 |
-6 |
3 |
|
A3 |
2 |
8 |
-1 |
-10 |
|
A4 |
-3 |
-9 |
-1 |
6 |
Вариант №14
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
-2 |
-4 |
|
A2 |
-2 |
2 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-5 |
-4 |
1 |
|
A2 |
-4 |
4 |
4 |
|
A3 |
1 |
0 |
-3 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
6 |
9 |
0 |
-9 |
|
A2 |
-8 |
-7 |
3 |
9 |
|
A3 |
-7 |
3 |
6 |
7 |
|
A4 |
-5 |
3 |
5 |
-5 |
Вариант №15
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
4 |
-1 |
|
A2 |
2 |
-1 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-1 |
0 |
-2 |
|
A2 |
4 |
3 |
-1 |
|
A3 |
-1 |
4 |
-4 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
6 |
-7 |
2 |
3 |
|
A2 |
-1 |
6 |
9 |
9 |
|
A3 |
8 |
-6 |
7 |
6 |
|
A4 |
7 |
-8 |
-1 |
-2 |
Вариант №16
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
4 |
4 |
|
A2 |
0 |
6 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
3 |
-3 |
0 |
|
A2 |
-5 |
-4 |
2 |
|
A3 |
-3 |
1 |
0 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
-7 |
2 |
3 |
4 |
|
A2 |
7 |
-4 |
-1 |
-6 |
|
A3 |
-7 |
6 |
7 |
6 |
|
A4 |
-4 |
5 |
-8 |
4 |
Вариант №17
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
2 |
2 |
|
A2 |
1 |
6 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-1 |
-4 |
2 |
|
A2 |
-5 |
-5 |
-3 |
|
A3 |
0 |
1 |
0 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
1 |
3 |
1 |
-4 |
|
A2 |
-3 |
4 |
1 |
-7 |
|
A3 |
-8 |
-10 |
5 |
9 |
|
A4 |
-6 |
0 |
9 |
1 |
Вариант №18
Задание №1.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | |
|---|---|---|
|
A1 |
-5 |
2 |
|
A2 |
1 |
0 |
Задание №2.
Для указанной матричной игры определите ее верхнюю и нижнюю цену, найдите оптимальные чистые (если они существуют), либо смешанные стратегии игроков А и В.
| B1 | B2 | B3 | |
|---|---|---|---|
|
A1 |
-2 |
0 |
-3 |
|
A2 |
2 |
2 |
-4 |
|
A3 |
-5 |
4 |
1 |
Задание №3.
Два конкурирующих друг с другом предприятия, выпускающие пылесосы, имеют следующие доли общего сбыта своей продукции на местном рынке: 53 % у предприятия 1 и 47 % - у предприятия 2. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: А1(В1) - расширить сеть сбыта; А2(В2) - реклама; А3(В3) - увеличить ассортимент(число моделей пылесосов); А4(В4) - ничего не предпринимать. Анализ показал, что изменения доли(в %) предприятия 1 на рынке в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими. Оценить эффективность проводимых мероприятий и изменение доли сбыта каждого предприятия на рынке.
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
|
A1 |
2 |
2 |
5 |
6 |
|
A2 |
3 |
2 |
-7 |
-5 |
|
A3 |
-1 |
9 |
-10 |
0 |
|
A4 |
0 |
-2 |
1 |
4 |
ВОПРОСЫ ВЫХОДНОГО КОНТРОЛЯ:
- Опишите понятие матричной игры.
- Опишите понятие стратегии матричной игры.
- Опишите понятие платежной матрицы матричной игры.
- Опишите правила выбора стратегии в матричной игре.
- Опишите понятие нижней и верхней цены матричной игры.
- Опишите понятие седловой точки матричной игры.
- Дайте понятие смешанной стратегии игрока в матричной игре.
- Приведите алгоритм решения матричной игры в смешанных стратегиях
ДОМАШНЕЕ ЗАДАНИЕ:
Выучить процесс поиска решения матричной игры в смешанных стратегиях.