ЭЛЕКТРОННЫЙ ЛАБОРАТОРНЫЙ ПРАКТИКУМ
ПО УЧЕБНОМУ ПРЕДМЕТУ
"ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ"
№21. Решение матричных игр с использованием графического метода
Цель: научить использовать графический метод для решения матричных игр.
Оборудование: практикум, тетрадь для лабораторных и практических работ.
Литература:
- Плотников А. Д. Математическое программирование: экспресс-курс. - Мн.: Новое знание, 2007. С. 147-156.
- Таха, Хемди. Введение в исследование операций - М.: Издательский дом "Вильямс", 2005. С. 446-465.
Время выполнения: 2 часа.
ВОПРОСЫ ВХОДНОГО КОНТРОЛЯ:
- Опишите понятие матричной игры.
- Опишите понятие стратегии матричной игры.
- Опишите понятие платежной матрицы матричной игры.
- Опишите правила выбора стратегии в матричной игре.
- Опишите понятие нижней и верхней цены матричной игры.
- Опишите понятие седловой точки матричной игры.
- Дайте понятие смешанной стратегии игрока в матричной игре.
- Приведите алгоритм решения матричной игры с использованием графического метода.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ:
Пусть игра задана платежной матрицей  . По оси абсцисс отложим единичный отрезок А1А2, где точка А1 (0, 0) изображает стратегию А1, А2 (1, 0) – стратегию А2, а каждая промежуточная точка SA этого отрезка изображает смешанную стратегию первого игрока PA = (p1, p2), где p1– расстояние от точки SA до A2, p2–расстояние от точки SA до A1. Выигрыш игрока A будем откладывать на вертикальных отрезках.
. По оси абсцисс отложим единичный отрезок А1А2, где точка А1 (0, 0) изображает стратегию А1, А2 (1, 0) – стратегию А2, а каждая промежуточная точка SA этого отрезка изображает смешанную стратегию первого игрока PA = (p1, p2), где p1– расстояние от точки SA до A2, p2–расстояние от точки SA до A1. Выигрыш игрока A будем откладывать на вертикальных отрезках.

Случай 1. Если игрок B применит стратегию В1, то выигрыш игрока A при стратегии А1 равен а11, поэтому на оси ординат отложим отрезок А1В1 = а11. При применении игроком A стратегии А2 выигрыш равен а21, отложим этот отрезок на перпендикуляре из точки А2, обозначим полученную точку В1'. Ордината любой точки М1 отрезка В1В1′ равна среднему выигрышу игрока A при применении смешанной стратегии SA(действительно, этот выигрыш равен математическому ожиданию случайной величины, т.е. a11p1 + a21p2). Запишем уравнение прямой В1В1′:
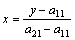 , т.е. y=a11+x(a21-a11),
, т.е. y=a11+x(a21-a11),
тогда при x = p2 получим
y = a11 + p2a21 – p2a11 = a11(1-p2) + p2a21 = a11p1 + a21p2
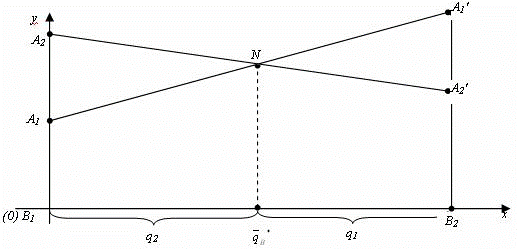
Случай 2. Если игрок B применяет стратегию В2, то аналогично откладываем отрезки а12 и а22 и получаем отрезок В2В2′. Ордината любой точки М2 отрезка В2В2′ – выигрыш игрока A, если A применяет смешанную стратегию SA, а B – стратегию В2. Построим нижнюю границу выигрыша игрока А – ломаную В1 NВ2′. Ординаты точек этой ломаной показывают минимальные выигрыши игрока А при использовании им любой смешанной стратегии. Оптимальное решение игры определяет точка N, в которой выигрыш игрока А принимает наибольшее значение. Ордината точки N равна цене игры. Проекция этой точки на ось ОХ показывает оптимальную стратегию (р1, р2).
Аналогично находится оптимальная стратегия Q = (q1 , q2) игрока B, только в соответствии с принципом минимакса надо находить верхнюю границу выигрыша, т. е. строить ломаную А2NА1′ и брать точку N с наименьшей ординатой.
Абсцисса точки N определяет оптимальную стратегию игрока B, т. е. Q = (q1 , q2).
МЕТОДИЧЕСКИЕ УКАЗАНИЯ:
Пример. Дана матричная игра с платёжной матрицей
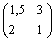
Найти ее решение графическим способом.
Решение.
Нижняя цена игры α = 1,5, верхняя цена игры β = 2. Так как α≠β, седловой точки нет. Так как a11 = 1,5, a21 = 2 строим точки B1(0;1,5) и B2(1;2), соединяем их отрезком. Так как a12 = 3, a22 = 1 строим точки B2(0;3) и B2’(1;1), соединяем их отрезком.
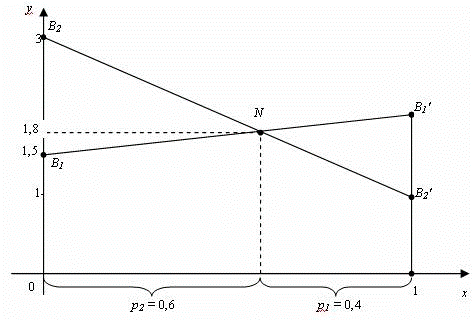
Уравнение прямой В1В1′:
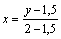 ,
,
т. е. y = 0,5x + 1,5;
уравнение В2В2′: 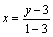 , т. е. y = 3-2x.
, т. е. y = 3-2x.
Найдем точку N пересечения прямых В1В1′ и В2В2′, для чего решим систему уравнений:
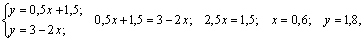
т. е. N(0,6; 1,8), откуда p2= 0,6; p1= 0,4; γ = 1,8 – цена игры.
Аналогично строим точки А1(0; 1,5) и А1′(1;3), А2(0; 2) и А2′(1; 1) и находим точку M пересечения прямых А1А1′ и А2А2′.
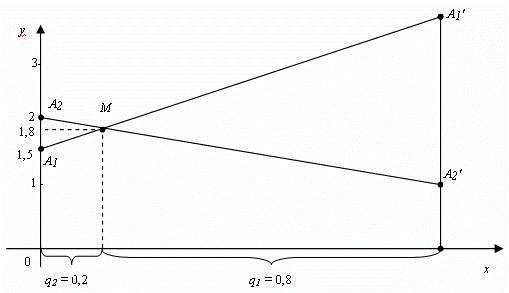
Ответ: смешанная стратегия игрока А: PA= (0,4; 0,6), игрока В: QB = (0,8; 0,2); цена игры 1,8.
СОДЕРЖАНИЕ РАБОТЫ:
Вариант №1
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 2,5 | 1,5 |
A2 | 4 | 1 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 4,5 | 3 |
A2 | 4 | 1 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 2,5 | 4,5 |
A2 | 2 | 4 |
Вариант №2
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 3 | 4,5 |
A2 | 3,5 | 2 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 1 | 1 |
A2 | 4 | 3,5 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 1 | 1 |
A2 | 2 | 2 |
Вариант №3
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 1,5 | 4,5 |
A2 | 2 | 3,5 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 1,5 | 1,5 |
A2 | 1 | 2,5 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 2,5 | 1,5 |
A2 | 1,5 | 3 |
Вариант №4
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 1 | 4 |
A2 | 3 | 1 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 3,5 | 2 |
A2 | 2 | 4 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 3 | 4,5 |
A2 | 3,5 | 1 |
Вариант №5
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 4,5 | 2,5 |
A2 | 3 | 3,5 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 3 | 1 |
A2 | 1,5 | 2,5 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 4 | 2,5 |
A2 | 4,5 | 4,5 |
Вариант №6
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 2 | 1,5 |
A2 | 4,5 | 2 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 4,5 | 4,5 |
A2 | 2,5 | 2,5 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 4 | 1 |
A2 | 1,5 | 1,5 |
Вариант №7
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 2,5 | 3,5 |
A2 | 4,5 | 3,5 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 3,5 | 3 |
A2 | 3,5 | 1,5 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 2 | 2 |
A2 | 3,5 | 3,5 |
Вариант №8
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 3 | 2 |
A2 | 4 | 2,5 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 4,5 | 3,5 |
A2 | 4 | 3 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 4 | 3,5 |
A2 | 4 | 3 |
Вариант №9
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 2,5 | 1 |
A2 | 4,5 | 3,5 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 3 | 1,5 |
A2 | 1,5 | 4 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 1,5 | 2 |
A2 | 2 | 4,5 |
Вариант №10
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 1 | 3 |
A2 | 3,5 | 2 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 3,5 | 3,5 |
A2 | 3,5 | 1 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 2,5 | 1,5 |
A2 | 3,5 | 3 |
Вариант №11
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 1,5 | 1 |
A2 | 3 | 1 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 2 | 3 |
A2 | 2,5 | 4 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 4,5 | 2,5 |
A2 | 2 | 3 |
Вариант №12
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 3,5 | 1 |
A2 | 3,5 | 1 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 1 | 4,5 |
A2 | 2,5 | 2 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 1 | 4,5 |
A2 | 2 | 2 |
Вариант №13
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 1 | 2,5 |
A2 | 4,5 | 1 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 4,5 | 4 |
A2 | 1 | 1,5 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 2,5 | 2 |
A2 | 2,5 | 2,5 |
Вариант №14
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 3,5 | 1,5 |
A2 | 2,5 | 3,5 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 4,5 | 2,5 |
A2 | 4,5 | 3,5 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 2 | 1 |
A2 | 3,5 | 3 |
Вариант №15
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 1 | 3,5 |
A2 | 1 | 3 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 4 | 2,5 |
A2 | 2,5 | 2 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 3,5 | 1,5 |
A2 | 1 | 4 |
Вариант №16
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 3,5 | 2 |
A2 | 4 | 1 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 2 | 1 |
A2 | 1,5 | 2 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 3 | 1,5 |
A2 | 2 | 4 |
Вариант №17
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 2,5 | 4 |
A2 | 2,5 | 3 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 4,5 | 3,5 |
A2 | 1 | 4,5 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 4 | 2 |
A2 | 1 | 2 |
Вариант №18
Решить матричные игры графическим методом.
№1.
| B1 | B2 | |
|---|---|---|
A1 | 4 | 3 |
A2 | 2,5 | 1 |
№2.
| B1 | B2 | |
|---|---|---|
A1 | 4 | 1,5 |
A2 | 4 | 3 |
№3.
| B1 | B2 | |
|---|---|---|
A1 | 1,5 | 3 |
A2 | 4,5 | 3 |
ВОПРОСЫ ВЫХОДНОГО КОНТРОЛЯ:
- Опишите понятие матричной игры.
- Опишите понятие стратегии матричной игры.
- Опишите понятие платежной матрицы матричной игры.
- Опишите правила выбора стратегии в матричной игре.
- Опишите понятие нижней и верхней цены матричной игры.
- Опишите понятие седловой точки матричной игры.
- Дайте понятие смешанной стратегии игрока в матричной игре.
- Приведите алгоритм решения матричной игры с использованием графического метода.
ДОМАШНЕЕ ЗАДАНИЕ:
Выучить процесс поиска решения матричной игры с использованием графического метода.